---

Was ist das Knotenpunktverfahren?

Mit dem Knotenpunktverfahren lassen sich alle Stabkräfte eines Fachwerks berechnen. Dafür muss jeder Knoten freigeschnitten wird. Anschließend werden die Gleichgewichts­bedingungen für jeden Knoten aufgestellt. Im Gegensatz zum Ritterschnitt­verfahren lassen sich mit dem Knotenpunktverfahren alle Stabkräfte berechnen.

---

Aufgabe: Stabkräfte berechnen

Das abgebildete Fachwerk ist fest-losgelagert und wird mit drei Kräften \( F_1,\,F_2,\,F_3 \) belastet. Zu berechnen sind die Stabkräfte der Stäbe 1-4 mittels Knotenpunktverfahren sowie die Auflagerkräfte des Systems.

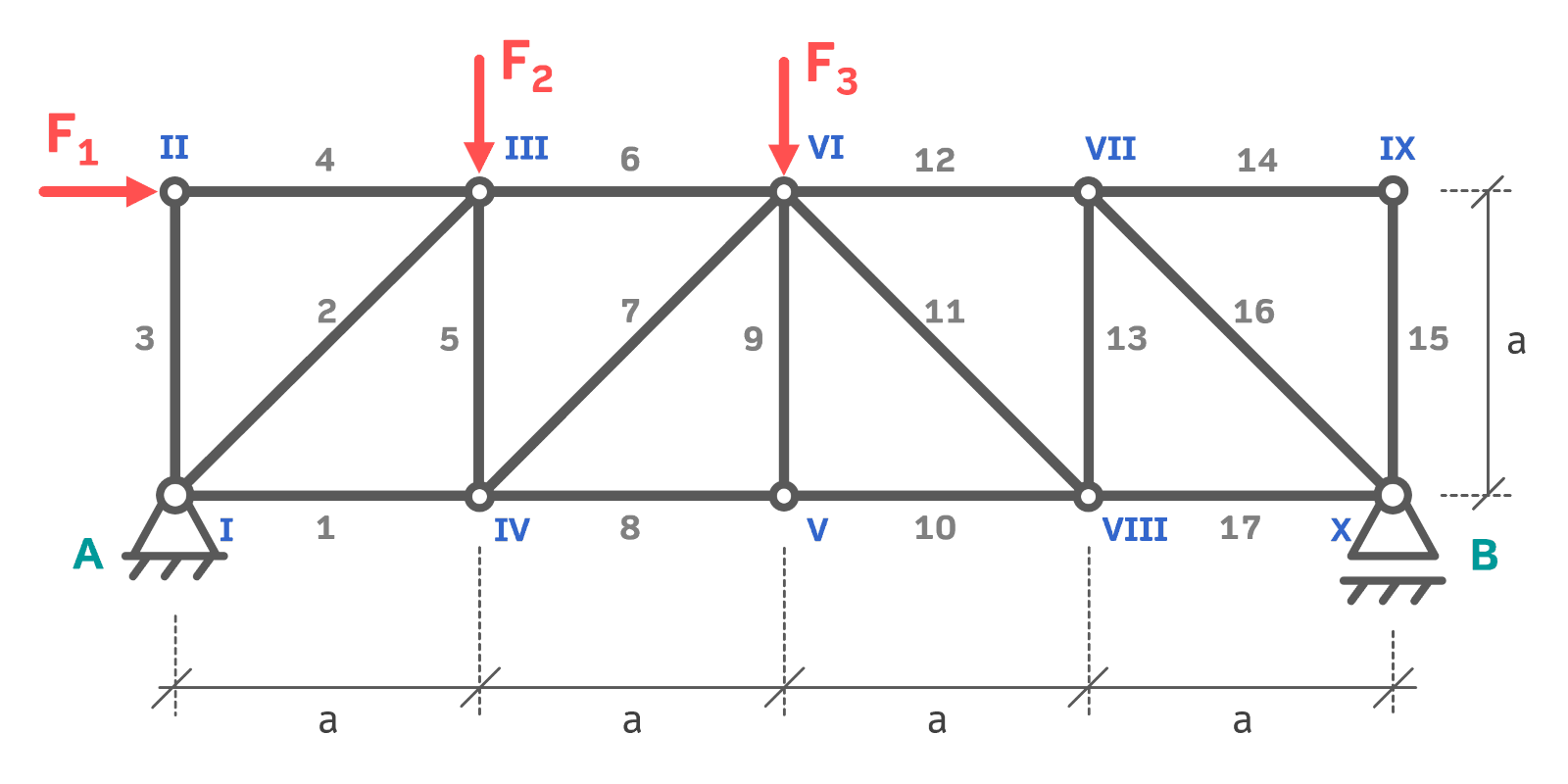
Gegeben: \( F_1=36\,kN,\,F_2=12\,kN,\,F_3=24\,kN,\,a=2\,m \)

---

Lösung per Knotenschnitt

Wir beginnen zuerst mit den Lagerkräften des Systems. Anschließend werden die Knoten der gesuchten Stäbe freigeschnitten, um die Stabkräfte zu berechnen.

Schritt 1: Auflagerkräfte berechnen

In den meisten Fällen müssen die Auflagerkräfte so oder so berechnet werden. Da es hier die Aufgabenstellung ohnehin fordert, beginnen wir mit den Auflagerkräften. Dazu wird das gesamte Fachwerk freigeschnitten (Freikörperbild). Aus den Gleichgewichts­bedingungen erhalten wir schließlich die Auflagerkräfte.

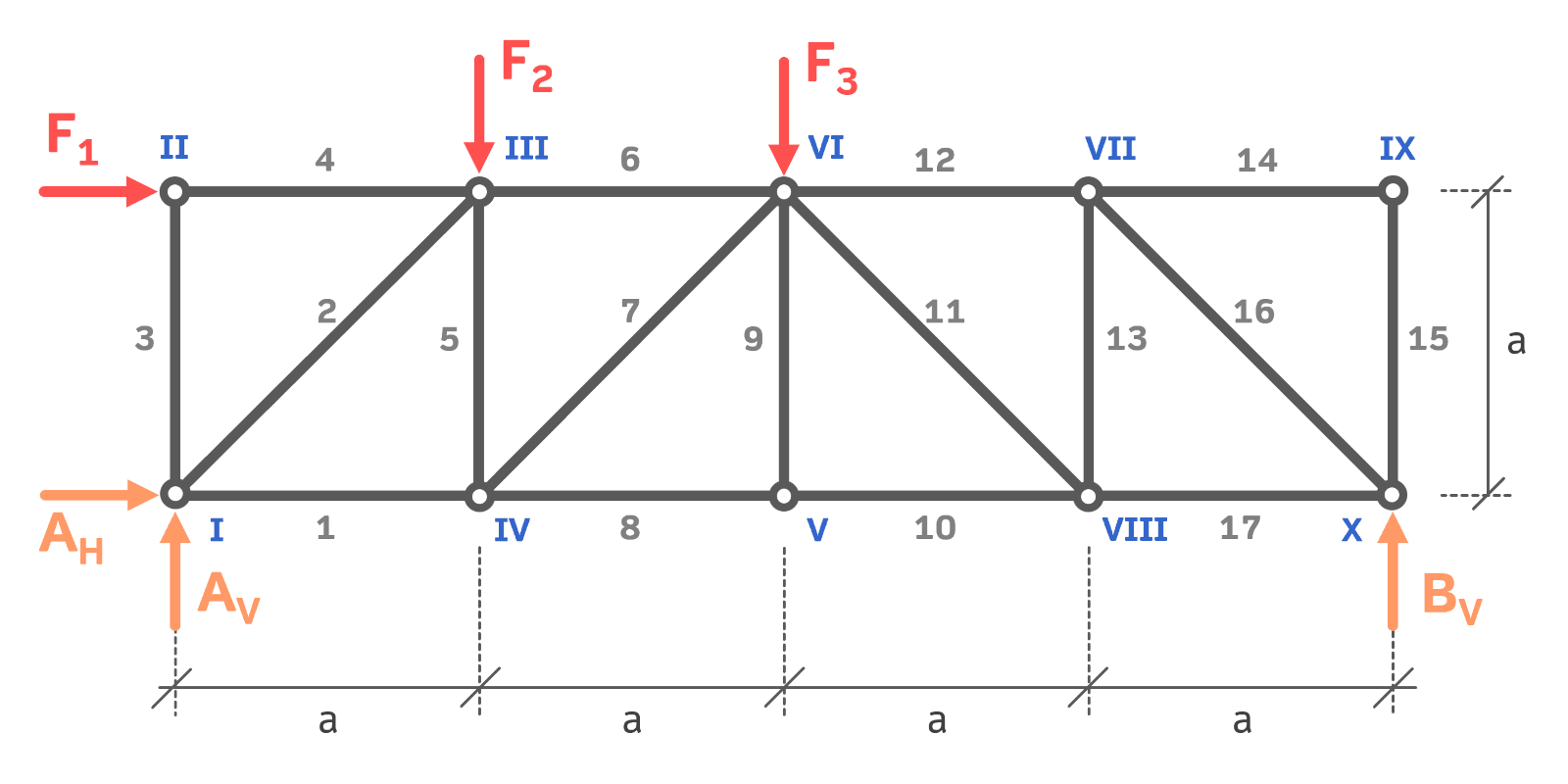
Summe aller Momente um Punkt A:
$$\sum M^A=0=B_V \cdot 4a-F_3 \cdot 2a-F_2 \cdot a-F_1 \cdot a$$ $$\Rightarrow B_V =\frac{1}{2}F_3+\frac{1}{4}F_2+\frac{1}{4}F_1=24\,kN$$
Summe aller Kräfte in horizontaler Richtung (x-Richtung):
$$\sum F_H=0=A_H+F_1$$ $$\Rightarrow A_H=-F_1=-36\,kN$$
Summe aller Kräfte in vertikaler Richtung (y-Richtung):
$$\sum F_V=0=A_V+B_V-F_2-F_3$$ $$\Rightarrow A_V=F_2+F_3-B_V=12\,kN$$

Schritt 2: Knotenpunktverfahren

Um die Stabkräfte mit dem Knotenpunktverfahren bzw. Knotenschnittverfahren zu bestimmen, müssen die betroffenen Knoten freigeschnitten werden. In diesem Fall sind die Stabkräfte 1-4 gesucht. Knoten I und II enthalten die gesuchten Stäbe. Knoten III enthält zwar auch gesuchte Stäbe (2 und 4), allerdings befinden sich an diesem Knoten auch die Stäbe 5 und 6, die nicht gesucht sind. Daher sind Knoten I und II zu bevorzugen.

Freischnitt Knoten II

Wir beginnen mit Knoten II, weil beim Knotenschnitt grundsätzlich ein Zentrales Kräftesystem vorliegt. Das bedeutet: Es stehen ledigleich zwei Kräftegleichgewichte zur Verfügung. Deswegen lassen sich maximal zwei unbekannte Stabkräfte pro Knoten berechnen. Mit Knoten I anzufangen würde nicht funktionieren, weil dort drei unbekannte Stabkräfte sind. Dafür ignorieren wir zu Übungszwecken die Tatsache, dass Stab 3 ein Nullstab und damit eigentlich bekannt ist.

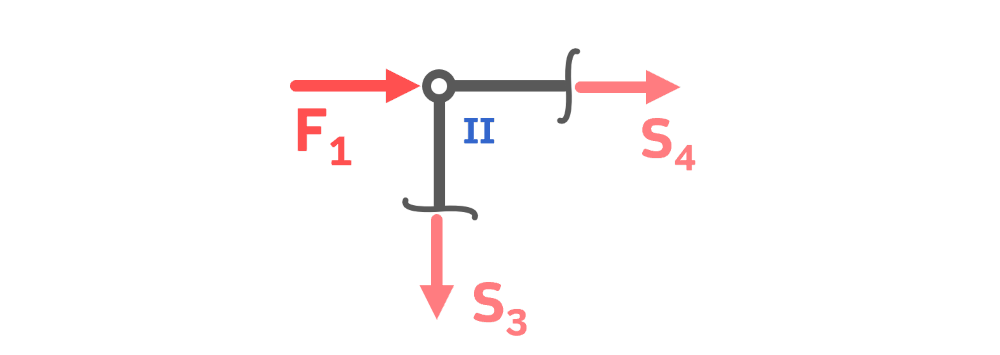
Summe aller Kräfte in horizontaler Richtung (x-Richtung):
$$\sum F_H=0=F_1+S_4$$ $$\Rightarrow S_4=-F_1=-36\,kN$$
Summe aller Kräfte in vertikaler Richtung (y-Richtung):
$$\sum F_V=0=-S_3\,\Rightarrow S_3=0$$

Stab 4 ist ein Druckstab (negatives Vorzeichen). Stab 3 ist ein Nullstab. Wie man sehen kann, liefert die Berechnung der Stabkräfte tatsächlich die Nullstäbe aus.

Freischnitt Knoten I

Jetzt sind am Knoten I nur noch zwei Stabkräfte unbekannt: Stabkraft 1 und 2. Bevor wir mit den Kräftegleichgewichten anfangen, sollte die schräge Stabkraft \( S_2 \) zerlegt werden. Zur Erinnerung: Kräftezerlegung (Grundlagen)

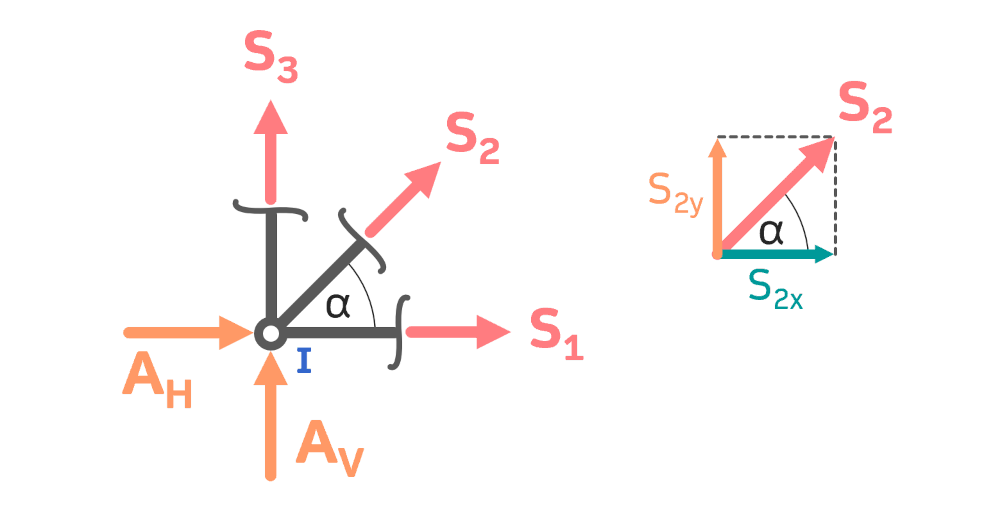Rechts im Bild dargestellt ist das Krafteck mit der zerlegten Kraft \( S_2 \). Die Kraftkomponenten sind

$$cos(\alpha)=\frac{S_{2x}}{S_2}\,\Rightarrow S_{2x}=S_2 \cdot cos(\alpha)$$
$$sin(\alpha)=\frac{S_{2y}}{S_2}\,\Rightarrow S_{2y}=S_2 \cdot sin(\alpha)$$

Den Winkel \( \alpha \) erhält man mit dem Tangens und dem rechtwinkligen Dreieck, das aus den Stäben 1, 2 und 5 besteht (siehe Fachwerk Aufgabenstellung):

$$tan(\alpha)=\frac{a}{a}=1\,\Rightarrow \alpha=45°$$

Jetzt, wo die schräge Stabkraft zerlegt und der Winkel bekannt ist, kann man die Stabkräfte mit den Kräftegleichgewichten berechnen:

Summe aller Kräfte in vertikaler Richtung (y-Richtung):
$$\sum F_V=0=A_V+S_3+S_{2y}$$ $$\Rightarrow S_{2y}=S_2 \cdot sin(\alpha)=-A_V-S_3$$ $$\Rightarrow S_2=\frac{-A_V-S_3}{sin(\alpha)}$$ $$S_2=-\sqrt{2} \cdot 12\,kN \approx -16,97\,kN$$
Summe aller Kräfte in horizontaler Richtung (x-Richtung):
$$\sum F_H=0=A_H+S_1+S_{2x}$$ $$\Rightarrow S_1=-A_H-S_{2x}$$ $$S_1=48\,kN$$

Stab 2 ist ein Druckstab (negatives VZ). Stab 1 ist ein Zugstab (positives VZ). Damit sind alle gesuchten Stabkräfte mit dem Knotenpunktverfahren bestimmt worden. Die Ergebnisse sind in der folgenden Tabelle zusammengefasst:

\[
\begin{array}{|c|c|c|}
\hline
Stab & Stabkraft\,[kN] & Zug/Druck \\
\hline
1 & 48 & Z \\
\hline
2 & -16,97 & D \\
\hline
3 & 0 & N \\
\hline
4 & -36 & D \\
\hline
\end{array}
\]

---

FAQ: Knotenpunktverfahren

Was ist mit den Auflagern?

Gute Frage! Für die Berechnung wird der Freischnitt bzw. das Freikörperbild betrachtet. Dort tauchen die Lager nicht mehr auf. Die Lagerstellen sind somit zu gewöhnlichen Knoten geworden (wie alle anderen Knoten auch). Außerdem wirken an den Lagerstellen die Lagerkräfte. Diese Kräfte werden so behandelt, als wären sie normale äußere Kräfte.

Was ist mit den Nullstäben?

Ausgezeichnete Frage! Natürlich macht es Sinn, vorher die offensichtlichen Nullstäben zu überprüfen, weil das einen kleinen Zeitvorteil verschafft. Wenn aber die Nullstäbe nicht erkannt werden, dann ist das nicht weiter schlimm. Durch die Berechnung der Stabkräfte erfahren wir so oder so, wenn ein Stab ein Nullstab ist. Weiterlesen: Nullstäbe erkennen

Spielt es eine Rolle, wie ich die Stabkräfte im Schnitt einzeichne?

Gute Frage! Ja, es spielt eine Rolle. In der Technischen Mechanik hat man sich darauf geeinigt, Stabkräfte so einzuzeichnen, dass sie vom Schnitt wegzeigen. Das ist praktisch, damit man Zugstäbe von Druckstäbe unterscheiden kann. Der Knotenschnitt wäre also falsch, wenn die Stabkräfte nicht in die vorgesehene Richtung zeigen.

---

Video: Fachwerke berechnen

In diesem Video wird ein Fachwerk Schritt für Schritt berechnet: Stabkräfte berechnen mit dem Knotenpunktverfahren und Nullstäbe erkennen mit den Nullstab-Regeln.

---

Zusammenfassung Knotenpunktverfahren

1. Lagerkräfte berechnen
2. Knoten freischneiden mit maximal 2 unbekannten Stabkräften
3. Zwei Kräftegleichgewichte aufstellen (\( \Sigma F_x,\:\Sigma F_y \)) und daraus die Stabkräfte ermitteln
4. Schritt 2 und 3 wiederholen, bis alle gesuchten Stabkräfte berechnet wurden

---

Verwandte Themen

Stabkräfte berechnen mit dem Ritterschnittverfahren
Nullstäbe erkennen (Nullstab-Regeln)
Kräftezerlegung
Zentrales Kräftesystem
Oder zurück zur Themenübersicht: Technische Mechanik 1