Lagerkräfte berechnen
Hier lernst du anhand eines Einführungsbeispiels, wie man Lagerkräfte berechnen kann. Betrachtet wird ein fest-los-gelagerter Balken, der mit einer Kraft \( F \) belastet wird. Außerdem werden die Lagerkräfte experimentell mithilfe von zwei Waagen ermittelt, um Lager bzw. Auflager besser zu verstehen.
Was ist eine Lagerkraft?
Kräfte die ein Lager aufnehmen kann, werden Lagerkräfte oder Lagerreaktionen genannt. Man nennt sich Lagerreaktionen, weil sie auf äußere Belastungen reagieren.
Aufgabe: Lagerkräfte berechnen
Der abgebildete Balken mit der Länge \( L \) ist auf einer Fest-Los-Lagerung befestigt und wird mit der Kraft \( F \) in der Balkenmitte belastet. Zu Berechnen sind die Lagerkräfte \( A_H,\:A_V,\:B_V \) des Systems.
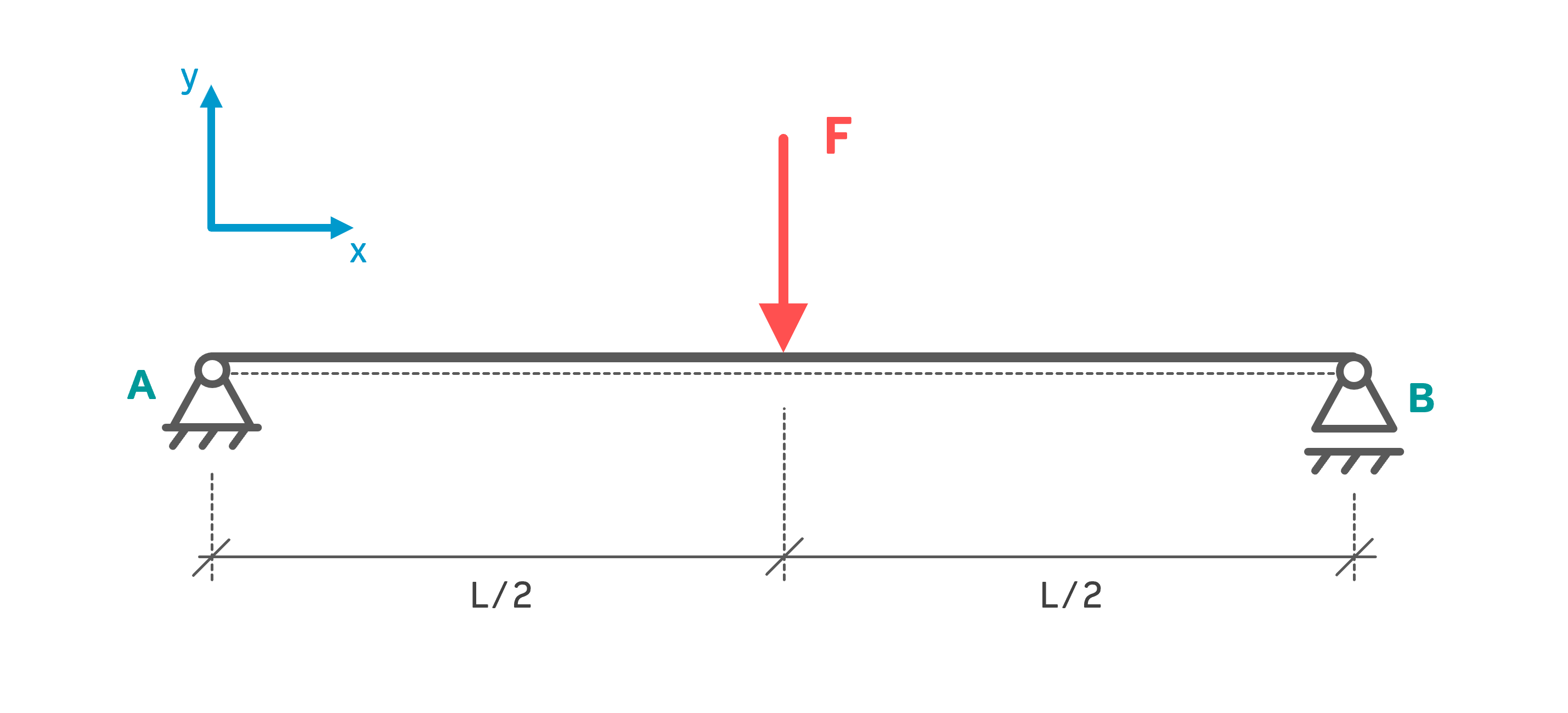
Gegeben: \( F=10\,kN,\; L=10\,m \)
Lösung: Lagerkräfte berechnen
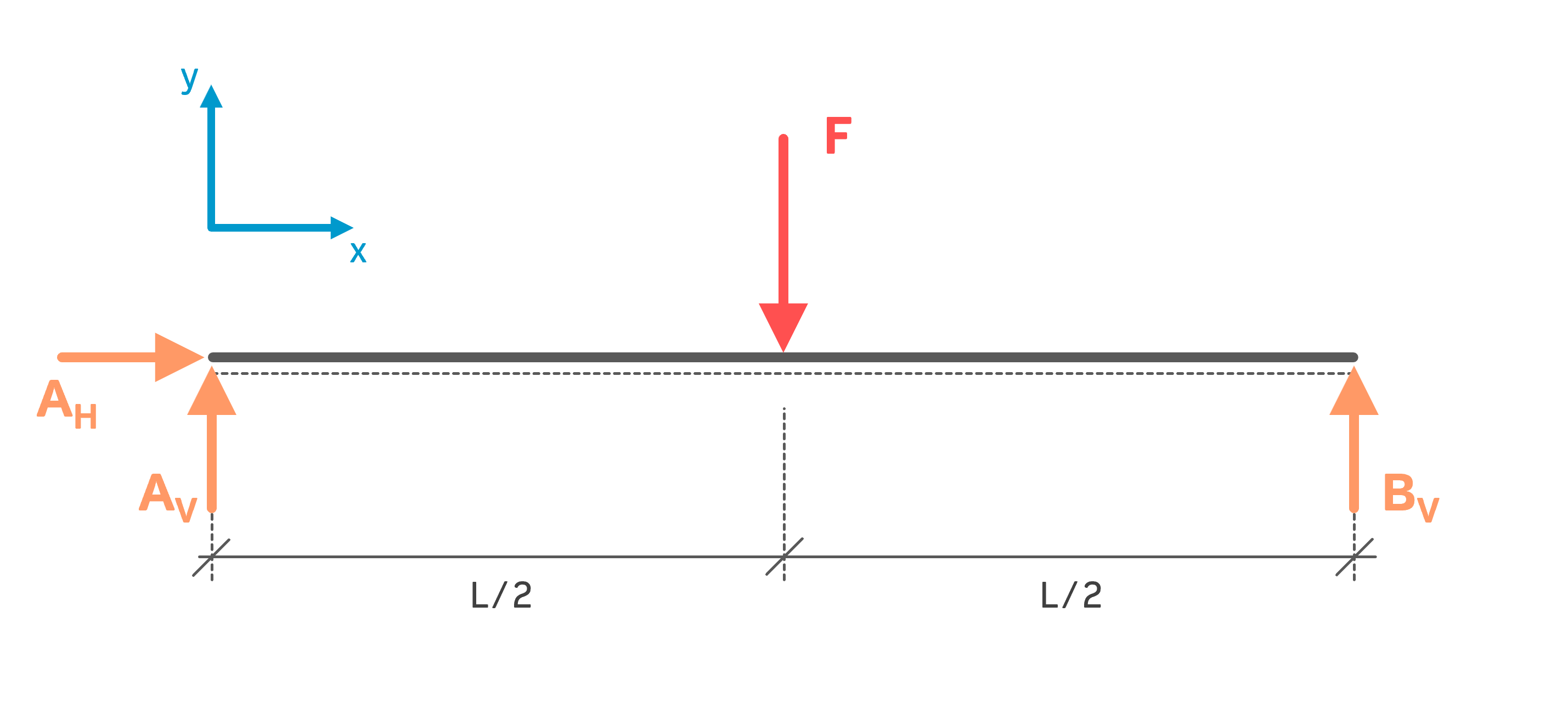
Schritt 1: Freischneiden
Dazu werden die Lager durch die entsprechenden Lagerkräfte ersetzt. Das Festlager ist zweiwertig und bekommt eine Horizontal- und eine Vertikalkraft. Das Loslager ist einwertig und bekommt nur eine Vertikalkraft. Das zugehörige Bild wird Freischnitt oder Freikörperbild genannt.
Schritt 2: Gleichgewichtsbedingungen aufstellen
Jede Gleichgewichtsbedingung liefert eine gesuchte Lagerkraft. Drei Gleichgewichte für drei Lagerreaktionen. Um die gesuchten Lagerkräfte zu erhalten, muss man für den Freischnitt aus dem vorherigen Schritt die Gleichgewichtsbedingungen aufstellen und sie nach den unbekannten Lagerkräften umstellen.
Summe aller Momente um Punkt A:
$$\sum M^A=0=B_V \cdot L-F \cdot \frac{L}{2}$$ $$\Rightarrow B_V \cdot L=F \cdot \frac{L}{2}$$ $$\Rightarrow B_V = \frac{F}{2}=5\,kN$$
Summe aller Kräfte in x-Richtung (Horizontalkräfte):
$$\sum F_H=0=A_H$$ $$\Rightarrow A_H=0$$
Summe aller Kräfte in y-Richtung (Vertikalkräfte):
$$\sum F_V=0=A_V+B_V-F$$ $$\Rightarrow A_V=F-B_V=\frac{F}{2}=5\,kN$$
Damit ist \( A_V=B_V \), was bedeutet, dass die beiden Auflager gleichmäßig belastet werden.
Video zu dieser Aufgabe
In diesem Video wird schrittweise erklärt, wie man die Lagerkräfte an einem Balken berechnen kann, an dem eine Strekenlast und eine Einzellast einwirken.
Mit dem Laden des Videos akzeptieren Sie die Datenschutzerklärung von YouTube.
Mehr erfahren
Zusammenfassung: Lagerkräfte berechnen
- Balken freischneiden und Lagerkräfte einzeichnen (in der Regel \( A_H,\:A_V,\:B_V \))
- Gleichgewichtsbedingungen aufstellen (\( \Sigma\:M,\:\Sigma F_x,\:\Sigma F_y \))
- Gleichgewichtsbedingungen nach den gesuchten Lagerkräften umstellen
Tipps für die Klausur
Reihenfolge bei den Gleichgewichtsbedingungen
Das Momentengleichgewicht als erstes aufstellen, weil man hier nur eine unbekannte Auflagerkraft in der Gleichung hat. Das bedeutet, dass man die gesuchte Auflagerkraft direkt erhält. Wer mit den beiden Kräftegleichgewichten anfängt, wird spätestens beim Kräftegleichgewicht in y-Richtung nicht mehr weiterkommen, weil dort zwei unbekannte Auflagerkräfte auftauchen, nämlich \( A_V \) und \( B_V \).
Symmetrie ausnutzen bei den Lagerkräften
Ist ein System symmetrisch und greift die äußere Belastung ebenfalls mittig an, dann sind die Kräfte an den Auflagern gleich groß und teilen sich die Belastung. Das unten gezeigte Bild mit den Küchenwaagen bestätigt die Annahme: Das Zahnrad wiegt \( 2\,kg \) und die beiden Auflager (also die Küchenwaagen) teilen sich die Last, weil die Waagen jeweils ca. \( 1\,kg \) anzeigen. Die Belastung fließt also zur Hälfte jeweils in die einzelnen Auflager. In der Klausur ist es oft erlaubt, vorhandene Symmetrien auszunutzen, um die Auflagerkräfte vereinfacht zu ermitteln. Allerdings muss man unbedingt auf die Symmetrie hinweisen. Ein solcher Hinweis könnte so aussehen: Aufgrund der Symmetrie ist \( A_V=B_V \).
Verwandte Themen
Statische Bestimmtheit
Lagerkräfte berechnen: Prüfungsaufgabe
Schnittgrößen berechnen
Oder zurück zur Themenübersicht: Technische Mechanik 1
