Schnittgrößenverläufe zeichnen (Beispiele)

Start › Lernplattform › Technische Mechanik 1 › Schnittgrößen › Schnittgrößenverläufe zeichnen (Beispiele)

Schnittgrößenverläufe zeichnen (Beispiele)

Auf dieser Seite kannst du dir einen Überblick darüber verschaffen, wie die Schnittgrößenverläufe aussehen, wenn verschiedene Belastungen auf verschiedene Systeme einwirken. Die häufigsten Belastungen sind Einzelkräfte, Streckenlasten und Drehmomente (bzw. Einzelmomente). Betrachtet werden die Schnittgrößenverläufe bei der klassischen Fest-Los-Lagerung und bei der festen Einspannung.

Inhaltsverzeichnis
  1. Schnittgrößenverläufe Fest-Los-Lagerung
  2. Schnittgrößenverläufe Einspannung
  3. Video: Schnittgrößen berechnen
  4. Verwandte Themen

Schnittgrößenverläufe Fest-Los-Lagerung

Beim fest-los-gelagerten Balken sollte man grob wissen, wie die Schnittgrößenverläufe bei den typischen Belastungen (Kraft, Streckenlast und Moment) aussehen.

Einzellast und Streckenlast

Schnittgrößenverläufe Überblick Tabelle Einzellast Kraft konstante Streckenlast
Bild 1: Schnittgrößenverlauf bei Kraft (l.) und Streckenlast (r.)
Erläuterung

Erläuterungen zur Einzellast

Greift eine Kraft (Einzellast) auf einen Balken an, dann macht die Querkraft einen Sprung – und zwar in Höhe der Kraft selbst, die an dieser Stelle angreift. Außerdem sorgt eine Einzellast für einen Knick im Momentenverlauf. Der Querkraftverlauf ist konstant und das Biegemoment verläuft linear (s. Bild 1, links). Das maximale Biegemoment ist dort wo die Einzellast wirkt. Wirken mehrere Lasten auf den Körper ein, dann lässt sich nicht mehr pauschal sagen, wo das maximale Moment ist. Eine Berechnung der Schnittgrößen gibt in diesem Fall Auskunft darüber: Schnittgrößen berechnen

Erläuterungen zur Streckenlast

Eine Gleichstreckenlast erzeugt im Allgemeinen im Querkraftverlauf immer einen Knick dort, wo die Streckenlast anfängt und aufhört. Dazwischen ist der Querkraftverlauf linear, sofern es sich um eine konstante Streckenlast handelt. Das Biegemoment ist dann quadratisch und das maximale Biegemoment ist dort, wo der Querkraftverlauf null ist bzw. wo die Querkraft ihre Nullstelle hat (s. Bild 1, rechts). Passend dazu: Schnittgrößen berechnen mit Gleichstreckenlast

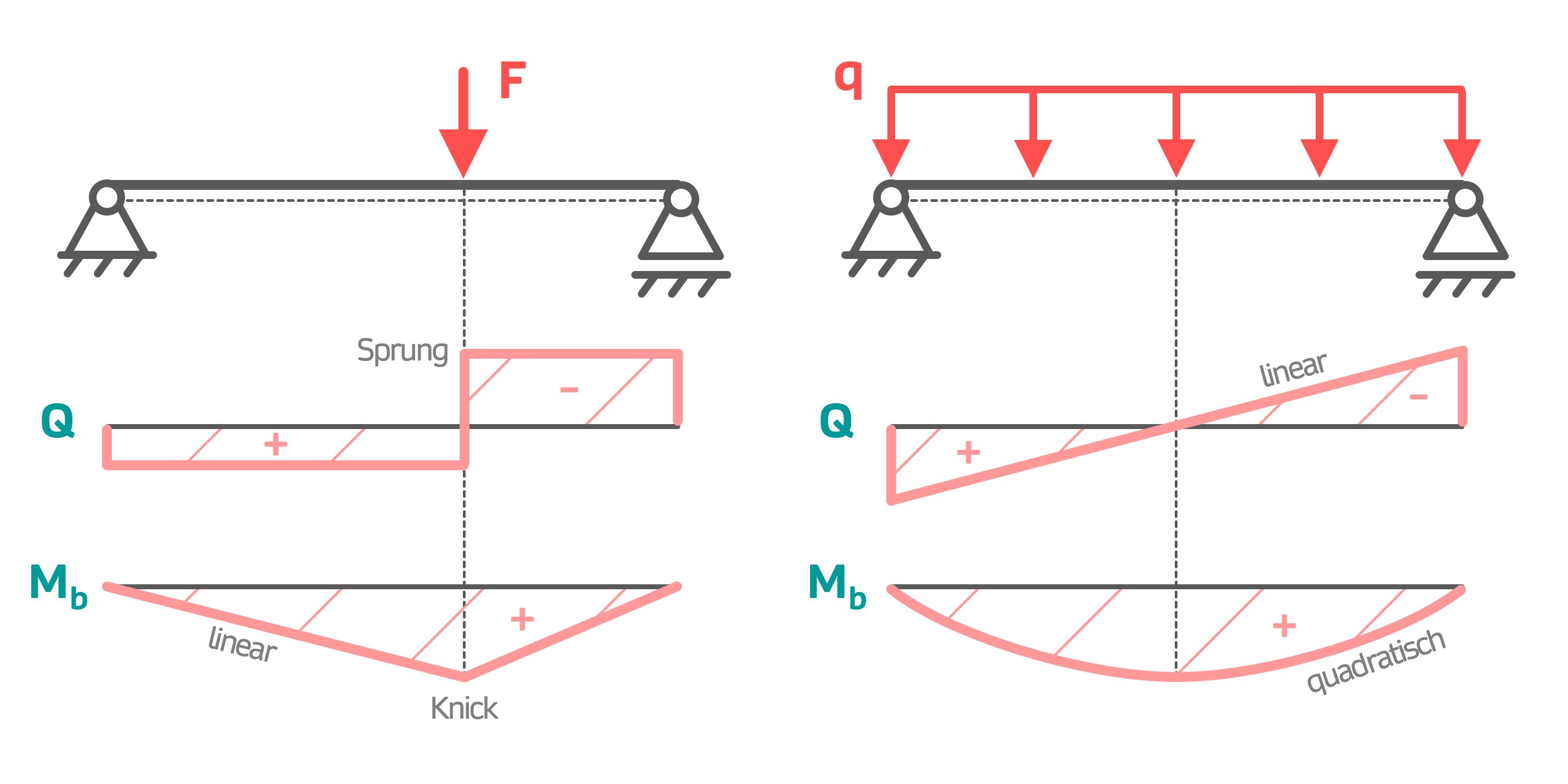
Diese Übersicht und mehr stehen dir auch in der kostenlosen Formelsammlung als pdf-Datei zum Download zur Verfügung: Formelsammlung Technische Mechanik 1

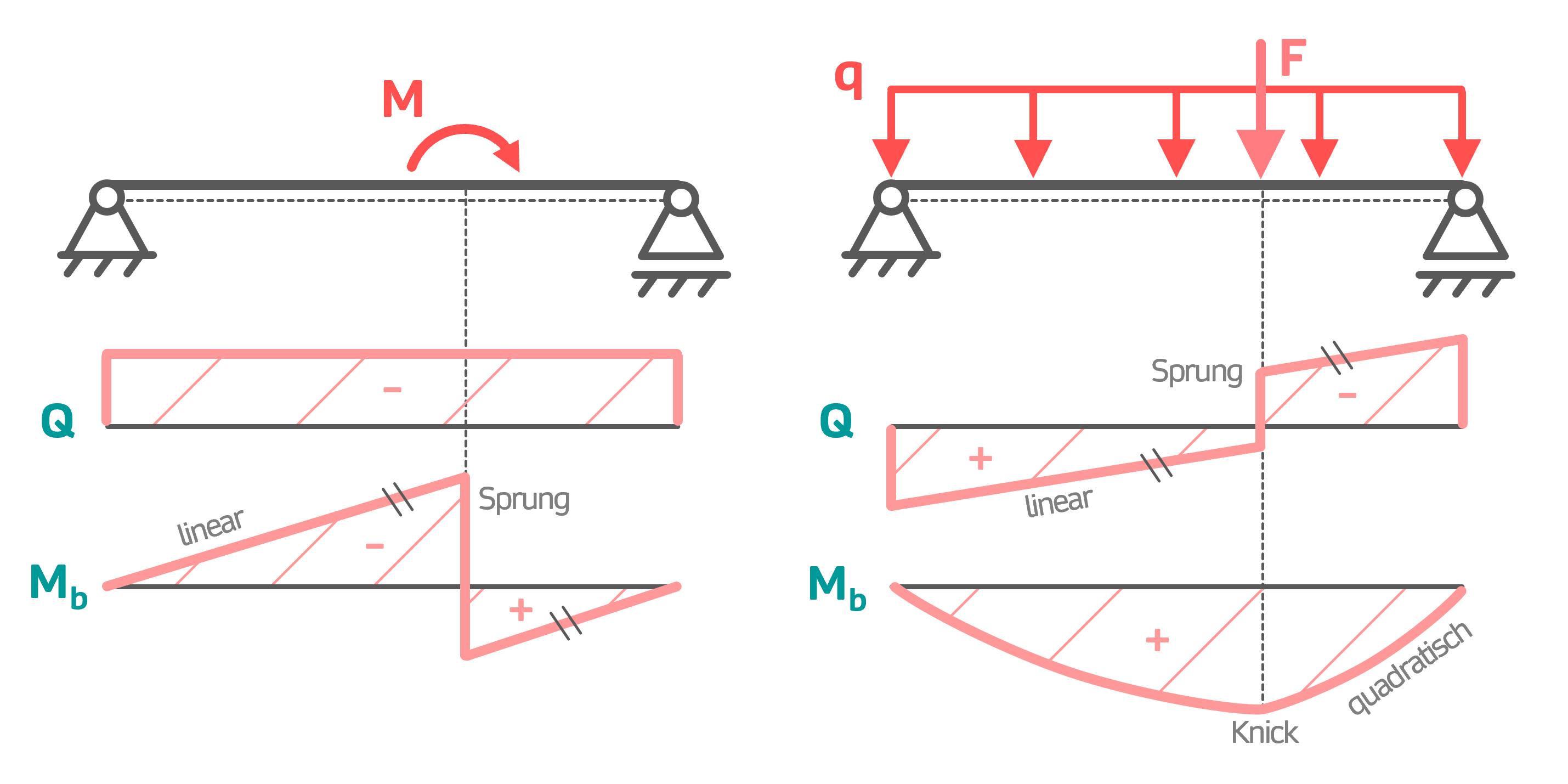
Drehmoment und kombinierte Last

Schnittgrößenverläufe Überblick Tabelle Drehmoment und Streckenlast mit Einzellast
Bild 2: Schnittgrößenverlauf bei Moment (l.) und kombinierter Last (r.)
Erläuterung

Erläuterungen zum Drehmoment

Ein einzelnes Drehmoment ruft eine konstante Querkraft hervor, siehe Bild 2 (links). Es kommt allerdings nicht zum Sprung oder Knicken des Querkraftverlaufs. Das Biegemoment hingegen verläuft linear und macht einen Sprung dort, wo das Drehmoment am Balken wirkt. Wichtig hierbei: Obwohl der Biegemomentenverlauf einen Sprung mittendrin macht, verlaufen die beiden linearen Abschnitte (links und rechts vom angreifenden Moment) parallel zueinander. Ein Drehmoment ist nebenbei bemerkt die einzige Möglichkeit, wie der Momentenverlauf einen Sprung macht.

Erläuterungen zur kombinierten Belastung

Im Prinzip ist bereits bekannt, wie die Schnittgrößenverläufe aussehen, wenn eine Streckenlast und eine Kraft kombiniert wirken: Die einzelnen Schnittgrößenverläufe für eine Streckenlast und für eine Einzellast werden einfach überlagert (siehe Bild 2, rechts). Das bedeutet die Querkraftlinie für die Streckenlast wird zu der Querkraftlinie für die Einzellast einfach dazuaddiert. Dasselbe wird auch mit der Momentenlinie gemacht. Superposition bzw. Superpositionsprinzip wird es in der Technischen Mechanik genannt. Bei einer Einzellast ist der Sprung bei der Querkraft und der Knick bei dem Biegemoment wichtig. Bei der konstanten Streckenlast ist der lineare Querkraftverlauf und der quadratische Momentenverlauf wichtig. All diese charakteristischen Merkmale tauchen im kombinierten Fall auf.

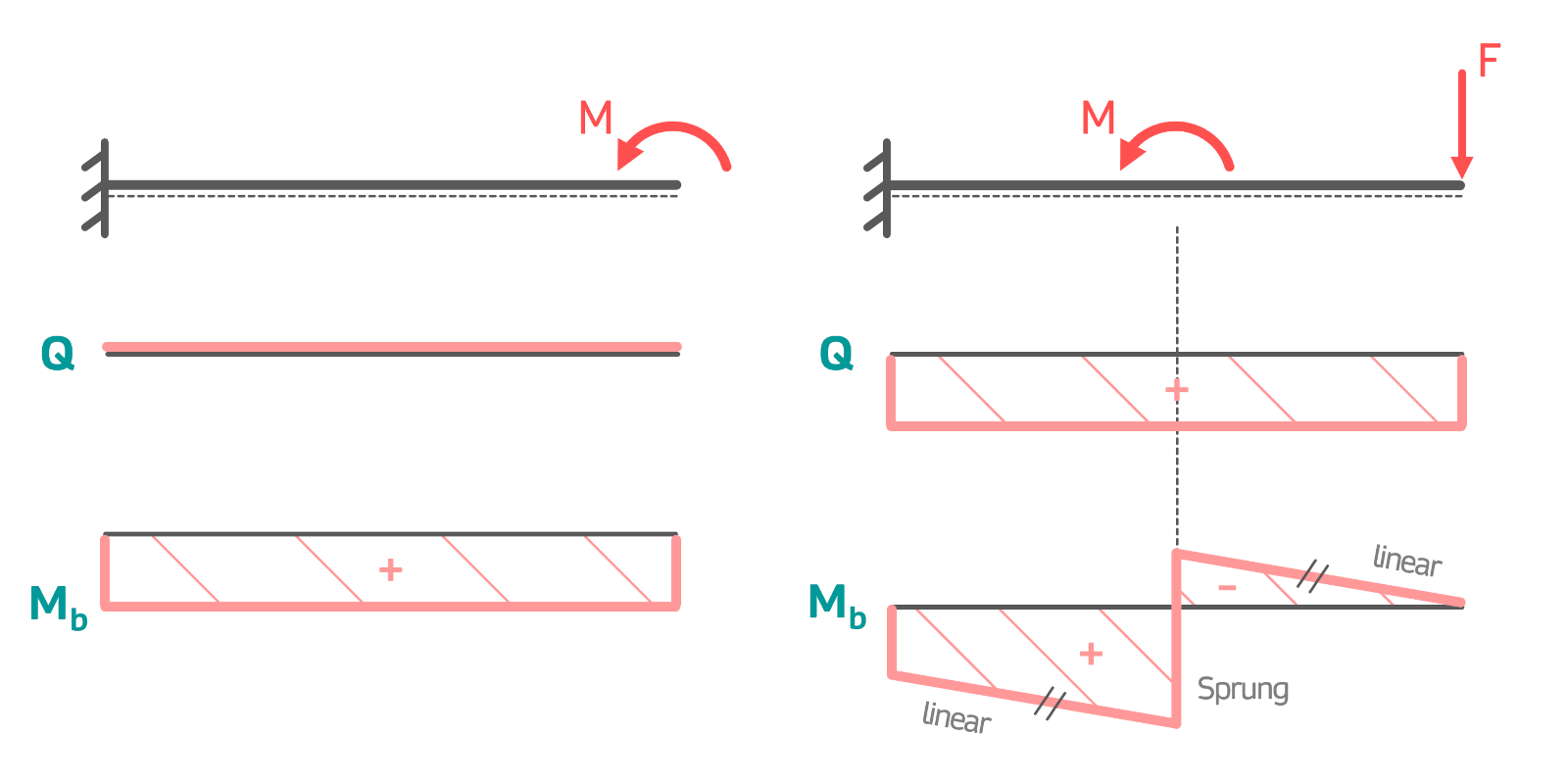
Schnittgrößenverläufe Einspannung

Auch beim eingespannten Balken bzw. bei der Einspannung sollte man grob wissen, wie die Schnittgrößenverläufe bei den typischen Belastungen (Kraft, Streckenlast und Moment) aussehen.

Einzellast und Streckenlast

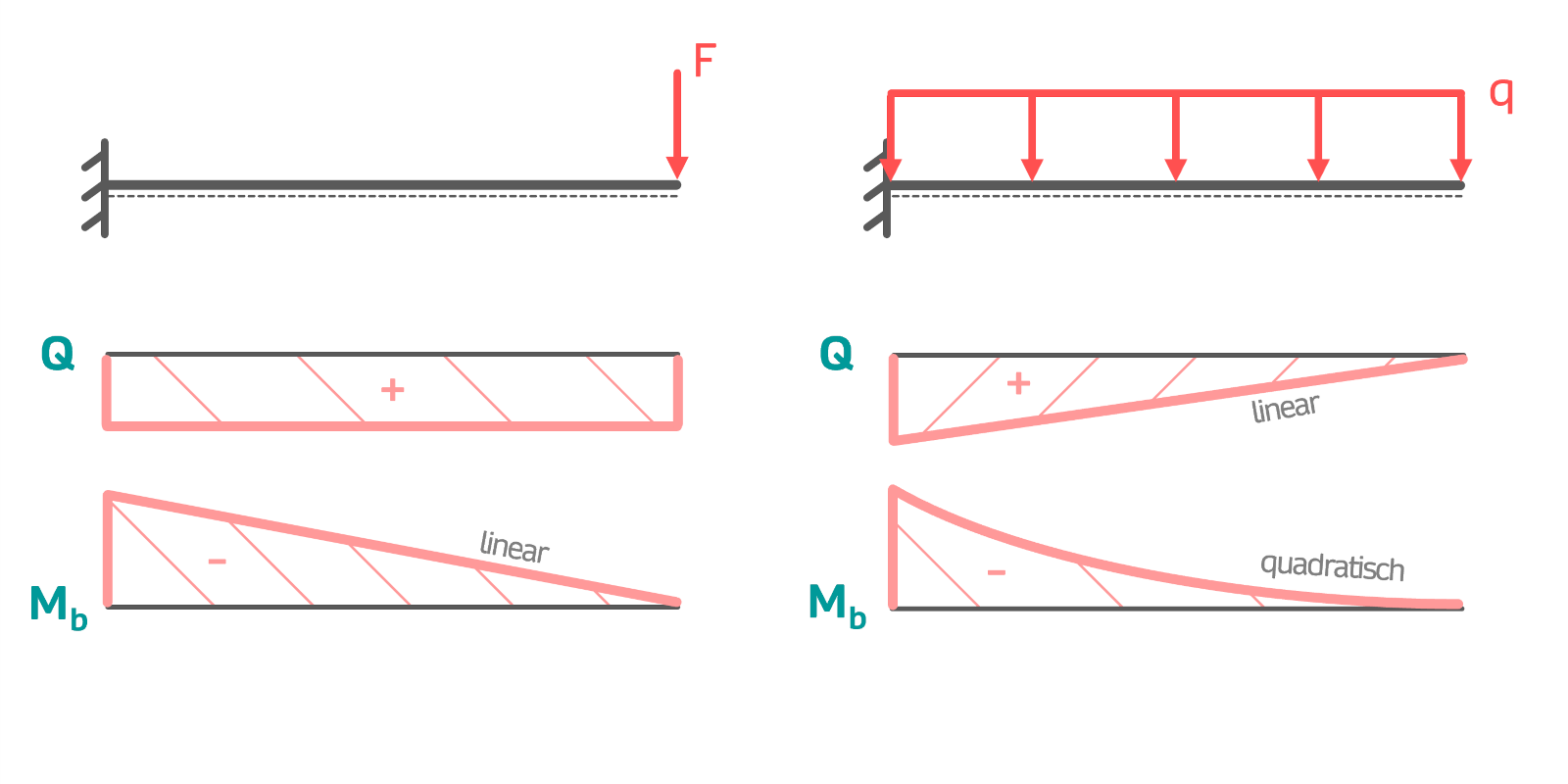
Schnittgrößenverläufe zeichnen Schnittgrößenverläufe Beispiele Schnittgrößen berechnen Streckenlast Einzellast Einspannung Fest Los Lagerung INGTUTOR
Bild 3: Schnittgrößenverläufe bei Einzellast (l.) und Streckenlast (r.)
Erläuterung

Erläuterungen zur Einzellast

Greift eine Kraft (Einzellast) auf einen Balken an, dann macht die Querkraft einen Sprung – und zwar in Höhe der Kraft selbst, die an dieser Stelle angreift. Außerdem sorgt eine Einzellast für einen Knick im Momentenverlauf. Der Querkraftverlauf ist konstant und das Biegemoment verläuft linear (s. Bild 3, links). Das maximale Biegemoment ist dort wo die Einspannung ist.

Erläuterungen zur Streckenlast

Eine Gleichstreckenlast erzeugt einen linearen Querkraftverlauf, der am freien Ende stets null ist (sofern dort keine Einzellast wirkt). Das Biegemoment verläuft quadratisch und hat an der Einspannung selbst seinen maximalen Wert. Das maximale Biegemoment befindet sich also an der Einspannung (s. Bild 3, rechts).

Drehmoment und kombinierte Last

Schnittgrößenverläufe zeichnen Schnittgrößenverläufe Beispiele Schnittgrößen berechnen Streckenlast Einzellast Einspannung Drehmoment Fest Los Lagerung INGTUTOR
Bild 4: Schnittgrößenverläufe bei Moment (l.) und kombinierter Last (r.)
Erläuterung

Erläuterungen zum Drehmoment

Ein einzelnes Drehmoment ruft eine konstante Querkraft hervor. Bei einer festen Einspannung ist die Querkraft (konstant) null, s. Bild 4 links. Das Biegemoment ist ebenfalls konstant. Allerdings ist das nur bei der Einspannung so. Die Schnittgrößenverläufe bei der Fest-Los-Lagerung (Einzellast, Streckenlast, Moment) sehen da anders aus. Dort ist das Biegemoment linear, wenn ein Moment den Balken belastet.

Erläuterungen zur kombinierten Belastung

Grundsätzlich ist schon bekannt, wie die Schnittgrößenverläufe aussehen, wenn eine Kraft und Moment kombiniert wirken: Die einzelnen Schnittgrößen für eine Einzellast und für ein Moment werden einfach überlagert (s. Bild 4, rechts). Das bedeutet die Querkraft für die Kraft wird zu der Querkraft für das Moment “dazuaddiert”. Dasselbe wird auch mit dem Biegemoment gemacht. Superposition wird dieses “dazuaddieren” in der Technischen Mechanik genannt. Bei einer Einzellast ist der lineare Verlauf des Biegemoments wichtig. Beim Moment ist der Sprung der Biegemomentenlinie wichtig. Diese charakteristischen Merkmale tauchen im kombinierten Fall auf.

Video: Schnittgrößen berechnen

In diesem Video erfährst du nochmal Schritt für Schritt, wie Schnittgrößen berechnet werden und wie die Schnittgrößenverläufe (Normalkraft, Querkraft und Biegemoment) gezeichnet werden.

YouTube

Mit dem Laden des Videos akzeptieren Sie die Datenschutzerklärung von YouTube.
Mehr erfahren

Video laden

Verwandte Themen

Formelsammlung Technische Mechanik 1 (pdf-Download)
Grundbegriffe Schnittgrößen
Schnittgrößen berechnen
Streckenlast berechnen: Formeln und Überblick
Oder zurück zur Themenübersicht: Technische Mechanik 1