Drehmoment berechnen
Das Drehmoment ist vermutlich die wichtigste Belastungsgröße in der Technischen Mechanik. Hier auf dieser Seite erfährst du was das Drehmoment ist, wie man das Drehmoment berechnen kann und was 1 Nm Drehmoment bedeutet.
Was versteht man unter Drehmoment?
Das Drehmoment ist definiert als Kraft mal Weg und verursacht eine Drehung (oder eine Biegung). Jede erdenkliche Drehbewegung ist von einem Drehmoment verursacht worden. Sei es das Öffnen einer Tür oder das Festdrehen einer Schraube. Die Einheit des Drehmoments ist \( Nm \) (Newtonmeter).
Vorgehen: Drehmoment berechnen
Um Drehmomente berechnen zu können, sind Kenntnisse über die einzelnen Bestandteile eines Moments notwendig. Zur Erläuterung des Begriffs Drehmoment dient ein Maulschlüssel.
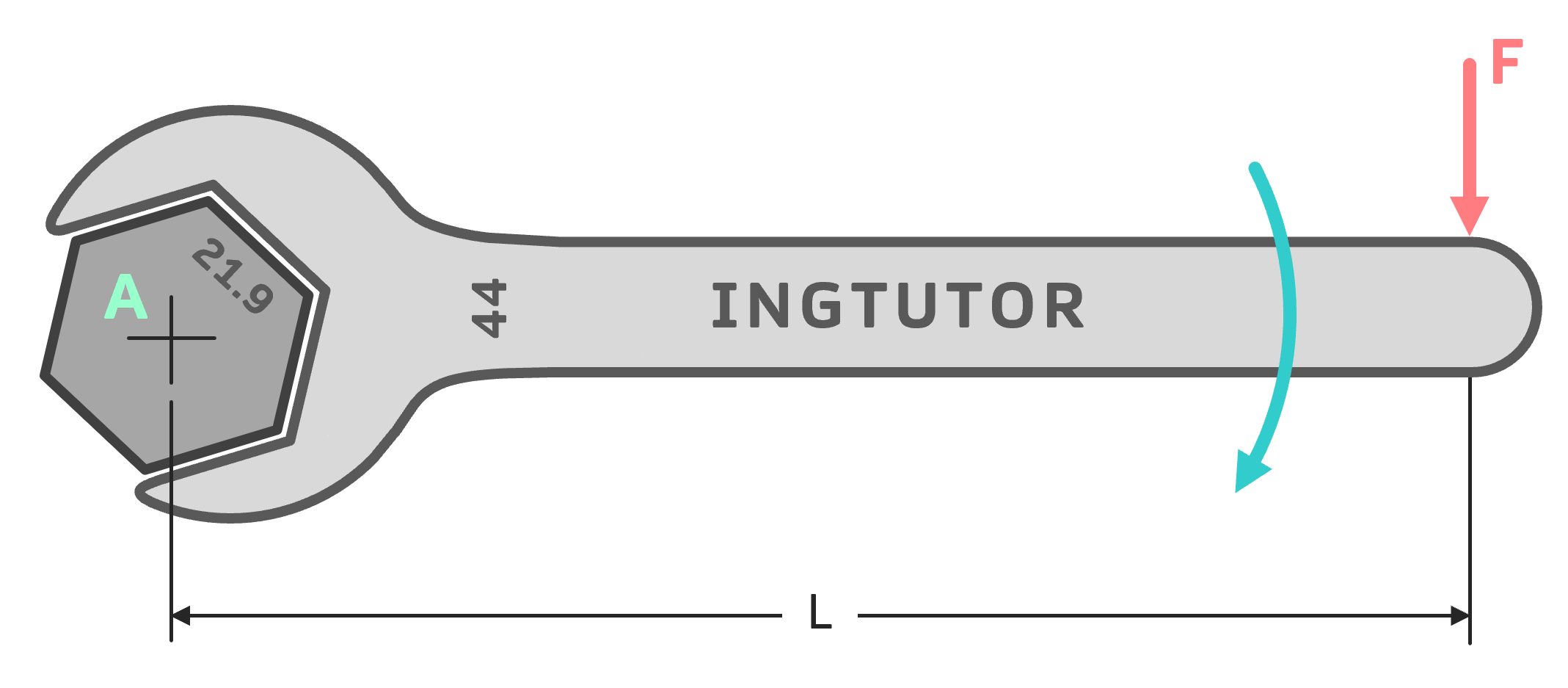Gegeben: \( F=100\,N,\,L=30\,cm \)
Schritt 1: Drehpunkt
Zunächst einmal muss der Drehpunkt erkannt oder festgelegt werden. Im Falle des Maulschlüssels liegt der Drehpunkt im Mittelpunkt der Schraube, da wir um diesen Punkt drehen müssen, um die Schraube festzuziehen. Diesen Punkt nennen wir A. Generell gilt: Der Drehpunkt befindet sich an dem Punkt, um den sich das System drehen wird.
Schritt 2: Kraft
Ist der Drehpunkt festgelegt, muss geprüft werden, ob die vorhandene Kraft eine Drehung verursacht. Alles was dafür nötig ist, ist eine Kraft, die nicht auf den Drehpunkt A zeigt. Jede Kraft, die diese Voraussetzung erfüllt, erzeugt nämlich ein Drehmoment und damit auch eine Drehung. Kräfte hingegen, die auf den Drehpunkt zeigen, erzeugen kein Drehmoment und keine Drehung. Die Kraft F in der Abbildung zeigt offensichtlich nicht auf den Drehpunkt A und erzeugt somit ein Drehmoment. Außerdem muss die Kraft stets senkrecht zum Hebelarm stehen. Dazu aber im nächsten Punkt mehr.
Schritt 3: Hebelarm
Nachdem Drehpunkt und Kraft abgehakt wurden, muss der Hebelarm geprüft werden. Der Hebelarm beim Drehmoment ist definiert als Abstand zwischen Drehpunkt und Kraft. Die Kraft steht dabei immer senkrecht auf den Hebelarm. Tut sie das nicht, muss sie mittels Kräftezerlegung so zerlegt werden, dass sie einen senkrechten Anteil zum Hebel hat, mit dem das Drehmoment berechnet wird. Grundsätzlich gilt: Je größer der Hebelarm, desto größer das Drehmoment. Die Hebellänge in diesem Beispiel ist der Abstand zwischen dem Drehpunkt A und der Kraft F, nämlich L.
Schritt 4: Kraft mal Weg
Wenn Drehpunkt, Kraft und Hebellänge bekannt sind, kann das Moment mit “Kraft mal Weg” ganz einfach berechnet werden:
$$M_A = F \cdot L = 100\,N \cdot 0,3\,m = 30\,Nm$$
Die Schraube wird also mit einem Drehmoment von 30 Nm festgezogen. Und damit ist das Drehmoment berechnet worden. Das A beim \( M_A \) bedeutet, dass das Drehmoment auf den Drehpunkt A bezogen ist. Diese Angabe ist freiwillig und hilft dem Leser lediglich zu verstehen, auf welchen Punkt sich das Moment bezieht.
Schritt 5: Drehsinn eines Moments
Hat man es mit mehreren Drehmomenten (oder Kräften, die eine Drehung verursachen) zu tun, dann spielt der Drehsinn des Moments eine wichtige Rolle. Man kann nämlich Drehmomente addieren oder voneinander abziehen – je nachdem, ob sie sich gegenseitig unterstützen oder sich gegenseitig aufheben. Das Rechenbeispiel im Anschluss verdeutlicht den Drehsinn eines Moments.
Übungsaufgabe: Kraft und Weg erkennen
Derselbe Maulschlüssel wird durch mehrere Kräfte an verschiedenen Stellen belastet. Es ist zu prüfen, welche Kräfte ein Drehmoment verursachen und welche nicht.
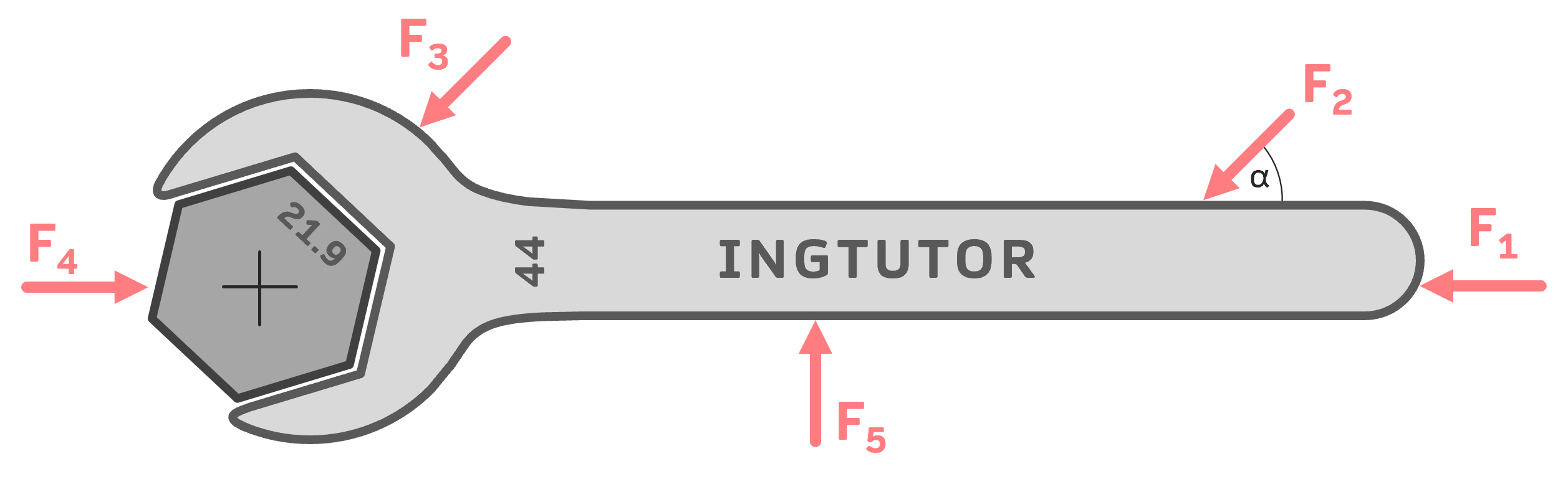
Lösung: Kraft und Weg erkennen
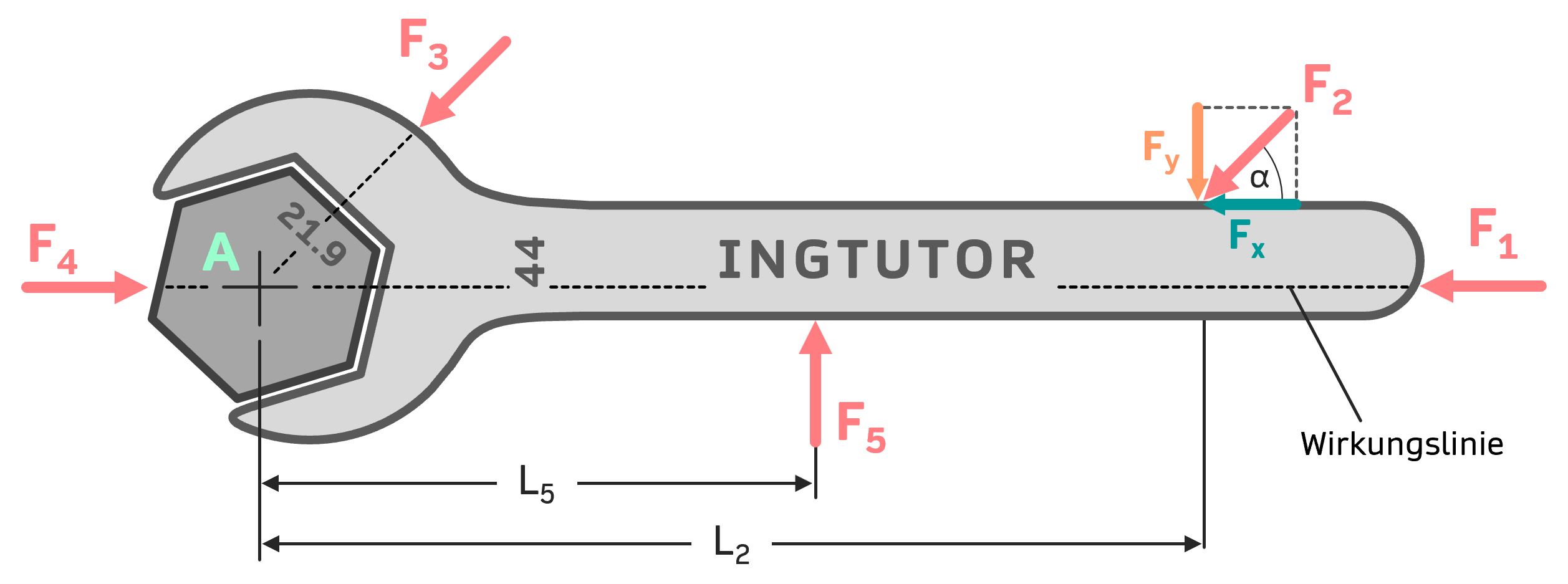
\( F_1 \), \( F_3 \), und \( F_4 \) erzeugen kein Moment
Diese drei Kräfte erzeugen kein Drehmoment, da sie direkt auf den Drehpunkt zeigen. Dementsprechend haben sie auch keine Drehwirkung. Die Wirkungslinien der drei Kräfte (gestrichelt dargestellt) zeigen deutlich, dass die Kräfte tatsächlich auf den Drehpunkt zeigen.
Bei \( F_2 \) wirkt nur der senkrechte Anteil
Die Kraft \( F_2 \) steht schräg auf den Hebelarm und muss erstmal so zerlegt werden, dass ein Anteil senkrecht zum Hebel steht: $$F_y = F \cdot sin(\alpha)$$ $$F_x = F \cdot cos(\alpha)$$
Wie man Kräfte genau zerlegt, kann hier in Ruhe wiederholt werden: Kräftezerlegung. Die Kräftezerlegung der Kraft \( F_2 \) hat schließlich eine senkrechte Kraftkomponente geliefert, mit der das Drehmoment berechnet werden kann. Zu der senkrechten Kraft \( F_y \) lässt sich sagen, dass sie nicht auf den Drehpunkt zeigt und damit ein Drehmoment verursacht: $$M_2=F \cdot sin(\alpha) \cdot L_2$$
Dieses Moment wirkt außerdem so, dass der Maulschlüssel nach unten gedreht wird (also im Uhrzeigersinn). Der Kraftanteil \( F_x \) ist parallel zum Hebel und zeigt auf den Drehpunkt. Damit erzeugt der parallele Anteil der Kraft \( F_2 \) kein Moment.
\( F_5 \) erzeugt ein negatives Moment
Die Kraft \( F_5 \) zeigt offensichtlich nicht auf den Drehpunkt und steht senkrecht auf den Hebelarm \( L_5 \), also auf den Abstand zwischen dem Drehpunkt A und der Kraft \( F_5 \). Das Drehmoment dieser Kraft ist
$$M_5 = F_5 \cdot L_5$$
Allerdings wirkt dieses Moment so, dass der Schlüssel nach oben gedreht wird (also gegen den Uhrzeigersinn). Damit wirkt das Moment \( M_5 \) gegen das Moment \( F_2 \). Wenn man die beiden Momente zusammenzählen möchte, geschieht dies so:
$$M_{ges}=M_2-M_5$$
Mit dem negativen Vorzeichen bei \( M_5 \) bringt man zum Ausdruck, dass dieses Moment eine negative Drehrichtung hat bzw. dass es entgegengesetzt zum (positiv wirkenden) Moment \( M_2 \) ist.
Rechenaufgabe: unbekannte Masse
Mithilfe eines Hebels wird eine schwere Masse mit bloßen Händen in Stellung gehalten. Es ist die unbekannte Masse des Körpers zu ermitteln.
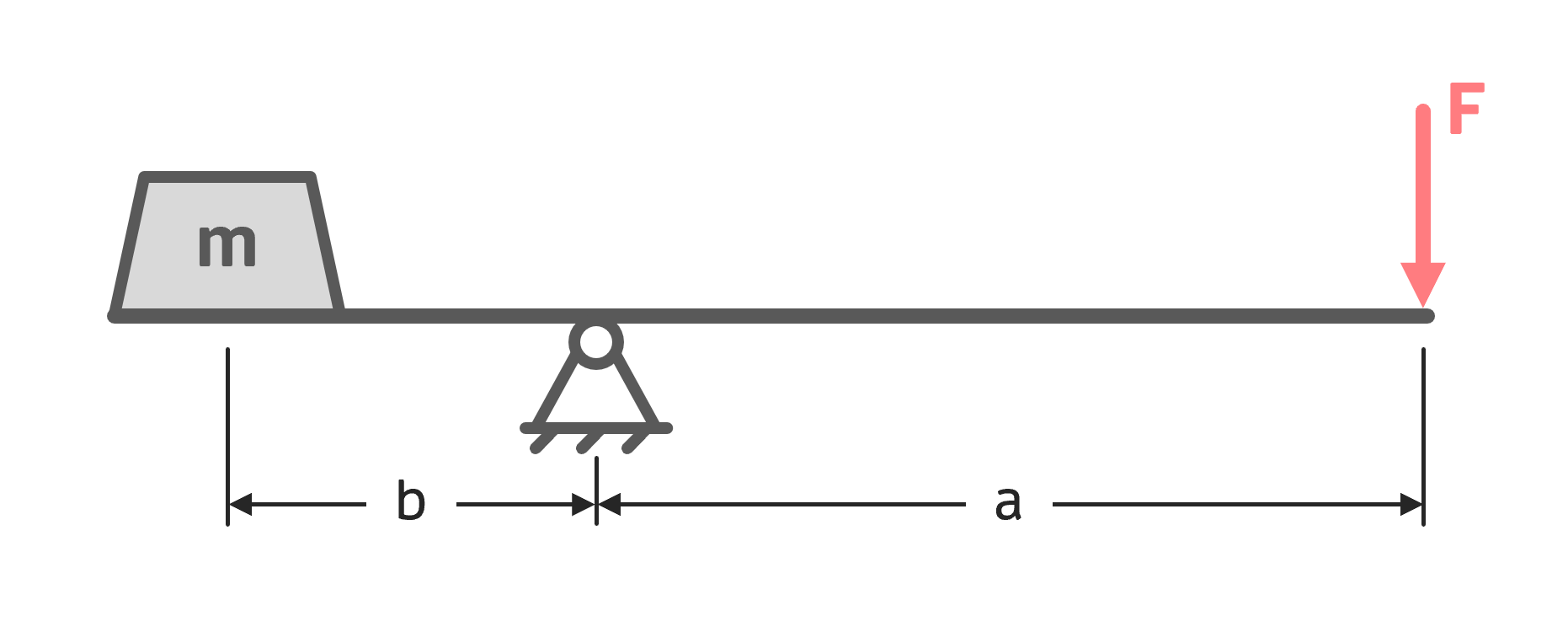Gegeben: \( F=400\,N\), \( a=5\,m \), \( b=1\,m \), \( g=10\,\frac{m}{s^2} \)
Lösung: unbekannte Masse
Zuerst ersetzen wir die unbekannte Masse durch die zugehörige Gewichtskraft \( F_g \). Außerdem deuten wir in der Skizze die Drehrichtung der beiden Kräfte an: Die Kraft \( F_g \) versucht den Hebel gegen den Uhrzeigersinn zu drehen. \( F \) hingegen versucht den Hebel im Uhrzeigersinn zu drehen. Der Drehpunkt ist offensichtlich der Punkt A. Die Abstände zwischen dem Drehpunkt und den Kräften sind a und b. Keine der beiden Kräfte zeigt auf den Drehpunkt oder steht schräg auf den Hebel.
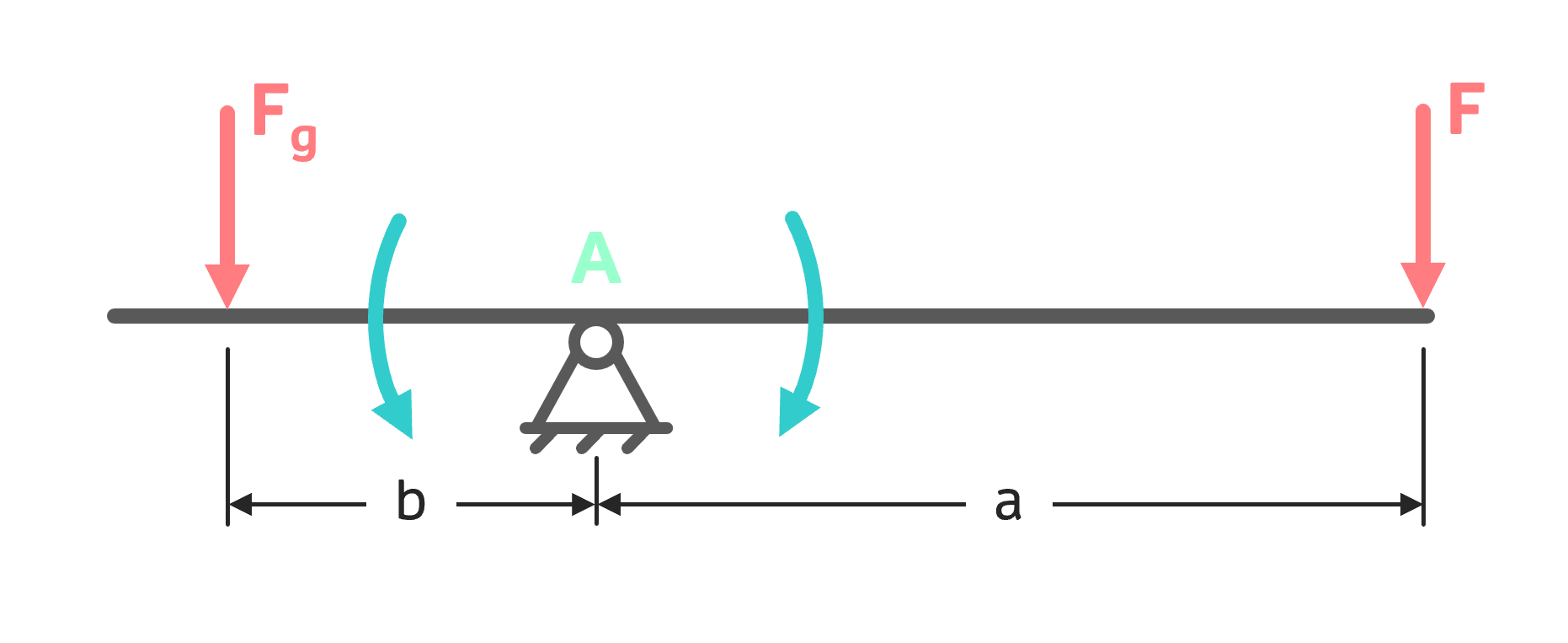
Momentengleichgewicht
Laut Aufgabenstellung steht der Hebel im Gleichgewicht. Die Summe der wirkenden Momente ist somit gleich null. Als Bezugspunkt für das Momentengleichgewicht ist der Drehpunkt A zu wählen. Der Uhrzeigersinn wird positiv definiert. Schließlich erhält man aus dem Momentengleichgewicht um Punkt A die Gewichtskraft:
$$\sum M^A=0=F \cdot a-F_g \cdot b$$ $$\Rightarrow F_g \cdot b=F \cdot a$$ $$\Rightarrow F_g = F \cdot \frac{a}{b}=2000\,N$$
Gewichtskraft
Um von der Gewichtskraft \( F_g \) auf die gesuchte Masse \( m \) zu kommen, braucht man die Formel
$$F_g = m \cdot g$$ Stellt man diese Gleichung nach der gesuchten Masse um, erhält man $$m = \frac{F_g}{g} = \frac{2000\,N}{10\,\frac{m}{s^2}} = 200\,kg$$
Zusammenfassung: Drehmomente berechnen
- Drehmoment ist Kraft mal Weg: $$M=F \cdot r$$
- Die Kraft steht dabei senkrecht auf den Hebel
- Der Hebel ist der Abstand zwischen der Kraft und dem Drehpunkt
- Drehmomente haben einen Drehsinn
- Zeigt eine Kraft auf den Drehpunkt, dann erzeugt sie kein Moment
- Steht eine Kraft schräg auf den Hebel, muss sie zerlegt werden (Kräfte zerlegen)
FAQ: Drehmoment berechnen
Wie rechnet man das Drehmoment aus?
Gute Frage! Das Drehmoment ist definiert als “Kraft mal Hebelarm”. Die Kraft steht dabei stets senkrecht auf den Hebel. Tut sie das nicht, muss sie zerlegt werden. Zeigt eine Kraft auf den Drehpunkt, dann ist das Drehmoment null. Mehr Infos zum Vorgehen findest du weiter oben unter Vorgehen: Drehmoment berechnen.
Was ist 1 Nm Drehmoment?
Ausgezeichnete Frage! 1 Newtonmeter bedeutet, dass eine Kraft von einem Newton auf einen Hebelarm mit einer Länge von einem Meter wirkt. $$M = 1\,N \cdot 1\,m = 1\,Nm$$ Man kommt aber auch mit folgender Konstellation darauf: $$M = 10\,N \cdot 10\,cm = 1\,Nm$$
Wie viel kg ist 1 Nm?
Gute Frage! Für die Umrechnung muss man wissen wie groß die Kraft ist, die 1 Nm Drehmoment erzeugt. Bei einem Hebelarm von 1 m wäre die zugehörige Kraft 1 N. Ein Newton (1 N) wiederum kann mit der Erdbeschleunigung g in eine Masse umgerechnet werden: $$F = m \cdot g$$ $$\Rightarrow m = \frac{F}{g} = \frac{1\,N}{10\,\frac{m}{s^2}} = 0,1\,kg$$
Video zum Thema Drehmoment
Dieses Video behandelt das Drehmoment und erklärt Schritt für Schritt wie man darauf kommt und wie man das Drehmoment berechnen kann.
Mit dem Laden des Videos akzeptieren Sie die Datenschutzerklärung von YouTube.
Mehr erfahren
Verwandte Themen
Kräftezerlegung
Lagerkräfte berechnen
Zentrales Kräftesystem
Oder zurück zur Themenübersicht: Technische Mechanik 1
