Reibung schiefe Ebene
Auf dieser Seite wird eine Übungsaufgabe zum Thema Reibung Schritt für Schritt und mit ausführlichem Lösungsweg berechnet. Eine Kiste auf einer schiefen Ebene wird gezogen. Zwischen der Kiste und dem Boden gibt es Reibung.
Was ist Reibung?
Kurzgesagt: Wenn zwei Körper Kontakt miteinander haben, dann entsteht Reibung. Das sind Kräfte, die so gerichtet sind, dass die der Bewegung entgegenstehen oder eine mögliche Bewegung verhindern. Dabei hängt die Reibung vor allem von der Oberfläche ab: Je rauer sie ist, desto größer die Reibung. Mehr zum Thema: Reibung (Grundlagen)
Aufgabe: Reibung schiefe Ebene
Eine Kiste der Masse \( m \) wird auf einer schiefen Ebene hochgezogen. Der Untergrund, auf dem die Kiste steht ist rau und somit reibbehaftet. Der Reibkoeffizient ist \( \mu \). Zu Ermitteln ist die Kraft \( F \), die benötigt wird, um die Kiste hochzuziehen.
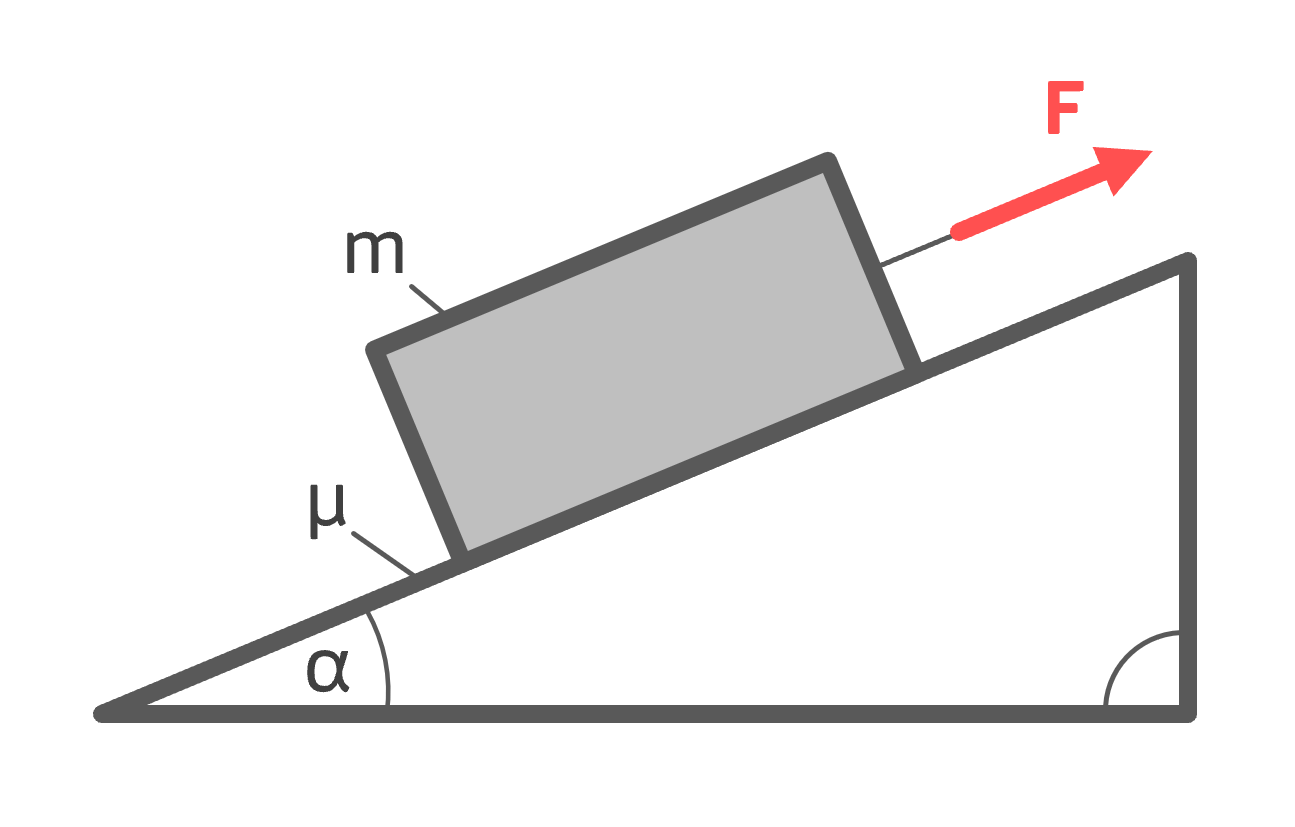Gegeben: \( m=100\,kg,\,\alpha=30°,\,g=9,81\,\frac{m}{s^2},\,\mu=0,3 \)
Lösung
Um die Kiste an der schiefen Ebene hochziehen zu können, muss die Gewichtskraft überwunden werden. Wegen dem rauen Untergrund wirkt zusätzlich Reibung. Die Reibkraft ist so gerichtet, dass sie der Aufwärtsbewegung entgegen wirkt.
Freischnitt
Wie immer, muss zunächst das Freikörperbild gezeichnet werden (Freischnitt).
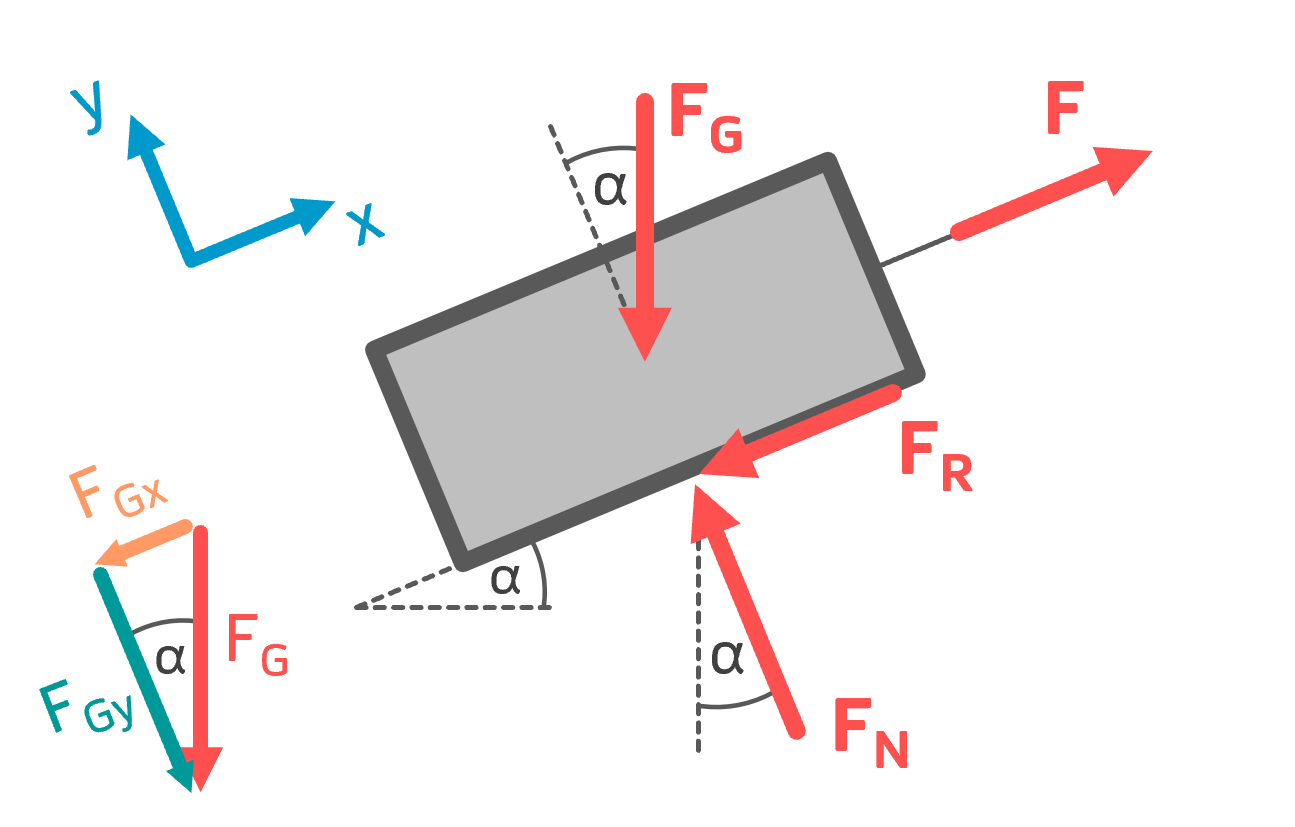
Zuerst wird ein x-y-Koordinatensystem eingeführt. Die x-Achse ist dabei parallel zur schiefen Ebene. Ein solches Koordinatensystem erleichtert die Kräftezerlegung. Außerdem muss darauf geachtet werden, dass die Reibkraft in die negative x-Richtung zeigt. Alle Kräfte, bis auf \( F_G \), zeigen in die x- oder y-Richtung und müssen daher nicht zerlegt werden.
Winkel richtig einzeichnen
Oft hilft eine kleine Animation, um die zusammenhängenden Winkel im System besser zu verstehen.
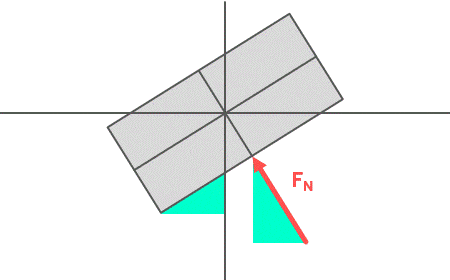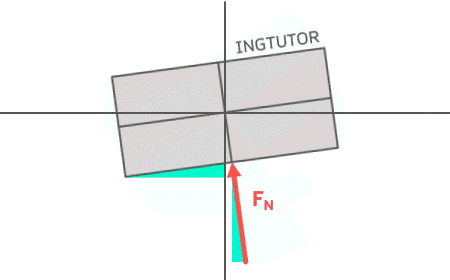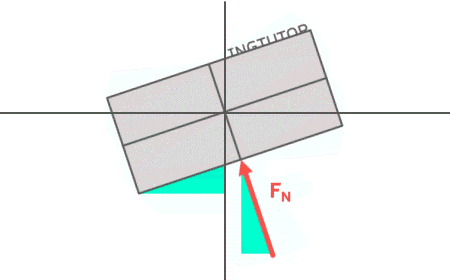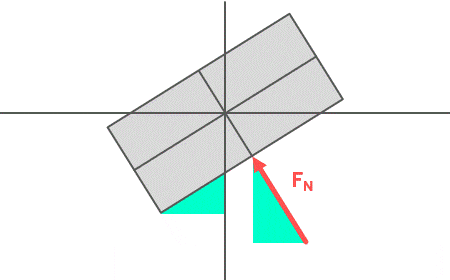
Hier zu sehen ist die Kiste in Schieflage mit der Normalkraft \( F_N \), die ja stets senkrecht auf die Unterseite der Kiste wirkt. Das grüne Dreieck bei \( F_N \) deutet das Kräftedreieck der Normalkraft an. Die Frage ist nun, an welcher Stelle im Kräftedreieck sich der Winkel \( \alpha \) befindet? Die Antwort ist ganz einfach: Verkleinert man den Winkel der schiefen Ebene, dann wird das linke Dreieck spitzer. Zeitgleich wird beim Kräftedreieck der obere Winkel an der Pfeilspitze von \( F_N \) ebenfalls kleiner. Man kann also feststellen: Der Winkel \( \alpha \) der schiefen Ebene befindet sich im Kräftedreieck oben an der Pfeilspitze von \( F_N \). Mit einer ähnlichen Überlegung kommt man auf den Winkel bei der Gewichtskraft \( F_N \).
Kräftezerlegung
Wie bereits erwähnt, zeigen 3 von 4 Kräfte entweder in die x- oder y-Richtung und müssen deshalb nicht zerlegt werden. Das ist auch der Grund, wieso ein gedrehtes x-y-Koordinatensystem gewählt wurde. Die übrig gebliebene Gewichtskraft \( F_G \) muss zerlegt werden, da sie einen x- und einen y-Anteil hat. Im Freikörperbild ist \( F_G \) bereits zerlegt (siehe Freischnitt). Rechnerisch gilt:
$$F_{Gx}=F_G \cdot sin(\alpha)=490,50\,N$$ $$F_{Gy}=F_G \cdot cos(\alpha)=849,57\,N$$
Einzelheiten zum Thema Kräftezerlegung sind hier: Kräfte richtig zerlegen
Gleichgewichtsbedingungen
Aus dem Kräftegleichgewicht in x-Richtung erhält man die gesuchte Kraft \( F \):
$$\sum F_x=0=F-F_R-F_{Gx}$$ $$\Rightarrow F=F_R+F_{Gx}$$
\( F_{Gx} \) wurde bei der Kräftezerlegung bereits bestimmt. Die Reibung \( F_R \) ist noch unbekannt und muss mithilfe der Normalkraft \( F_N \) bestimmt werden. Die Normalkraft erhält man aus dem Kräftegleichgewicht in y-Richtung:
$$\sum F_y=0=F_N-F_{Gy}$$ $$\Rightarrow F_N=F_{Gy}=F_G \cdot cos(\alpha)$$ $$F_N=849,57\,N$$
Reibung berechnen
Mithilfe des Reibungsgesetzes (Coulomb-Reibung) kann man aus der Anpresskraft auf dem Boden, also der Normalkraft, und dem Reibungskoeffizienten die Reibung berechnen:
$$F_R= \mu \cdot F_N$$ $$\Rightarrow F_R=254,87\,N$$
Jetzt, wo alle unbekannten Größen berechnet wurden, kann man die gesuchte Kraft \( F \) bestimmen.
Aus dem Kräftegleichgewicht in x-Richtung folgte:
$$F=F_R+F_{Gx}$$
Setzen wir nun die berechneten Größen ein, erhält man:
$$F=254,87\,N+490,50\,N$$ $$\Rightarrow F=745,37\,N$$
Die Kiste muss also mit einer Kraft von rund \( 745,37\,N \) gezogen werden, um die (anteilige) Gewichtskraft und die Reibung zu überwinden. Man kann die Gleichung für \( F \) auch erstmal zusammenfassen, um dann am Ende die Zahlenwerte einzusetzen. Das sieht dann so aus:
$$F=F_R+F_{Gx}$$ $$F=\mu \cdot F_N + F_G \cdot sin(\alpha)$$ $$F=\mu \cdot m \cdot g \cdot cos(\alpha) + m \cdot g \cdot sin(\alpha)$$ $$F=m \cdot g \cdot (\mu \cdot cos(\alpha) + sin(\alpha))$$
Und das führt wieder zur benötigten Kraft von
$$F=745,37\,N$$
Zusammenfassung: Reibkraft und Reibung
Aufgaben zum Thema Reibung oder Haftreibung können ganz unterschiedlich sein. Ein festes Vorgehen, wie beispielsweise bei der Berechnung von Schwerpunkten, gibt es aufgrund der Vielzahl an unterschhiedlichen Aufgaben hier nicht. Dennoch kann man sich an folgende Punkte orientieren, um eine klassische Reibungsaufgabe anzugehen.
- Das Reibungsgesetz lautet \( F_R = \mu \cdot F_N \)
- Dabei ist die Normalkraft \( F_N \) die Anpresskraft des Körpers auf dem Untergrund und lässt sich meist aus dem Kräftegleichgewicht in y-Richtung bestimmen.
- Die Reibung \( F_R \) steckt meist im Kräftegleichgewicht in x-Richtung.
- In der Regel muss man beide Kräftegleichgewichte aufstellen und zusätzlich das Reibungsgesetzt als dritte Gleichung nutzen, um die gesuchte Größe zu ermitteln.
- In manchen Fällen kann es notwendig sein, eine Momentengleichung aufzustellen.
Verwandte Themen
Grundlagen der Haftreibung und Reibung
Seilreibung und Seilhaftung
Kräftezerlegung
Lagerkräfte berechnen
Oder zurück zur Themenübersicht: Technische Mechanik 1
