Kräftezerlegung
Die Kräftezerlegung ist ein elementarer Bestandteil der Technischen Mechanik. Dabei werden die Kräfte meist in ihre Komponenten entlang der x- und y-Achse zerlegt. Es gibt nahezu keine Bereiche in der Technischen Mechanik, die ohne eine Zerlegung der Kräfte in die einzelnen Komponenten auskommen.
Was versteht man unter Kräftezerlegung?
Bei der Kräftezerlegung geht es darum, dass verschiedene Kräfte möglichst einfach zusammengerechnet werden können. Dafür zerlegt man schräge Kräfte in ihre einzelnen Komponenten (x- und y-Komponente). Dieser Prozess heißt Kräftezerlegung.
Vorgehen bei der Kräftezerlegung
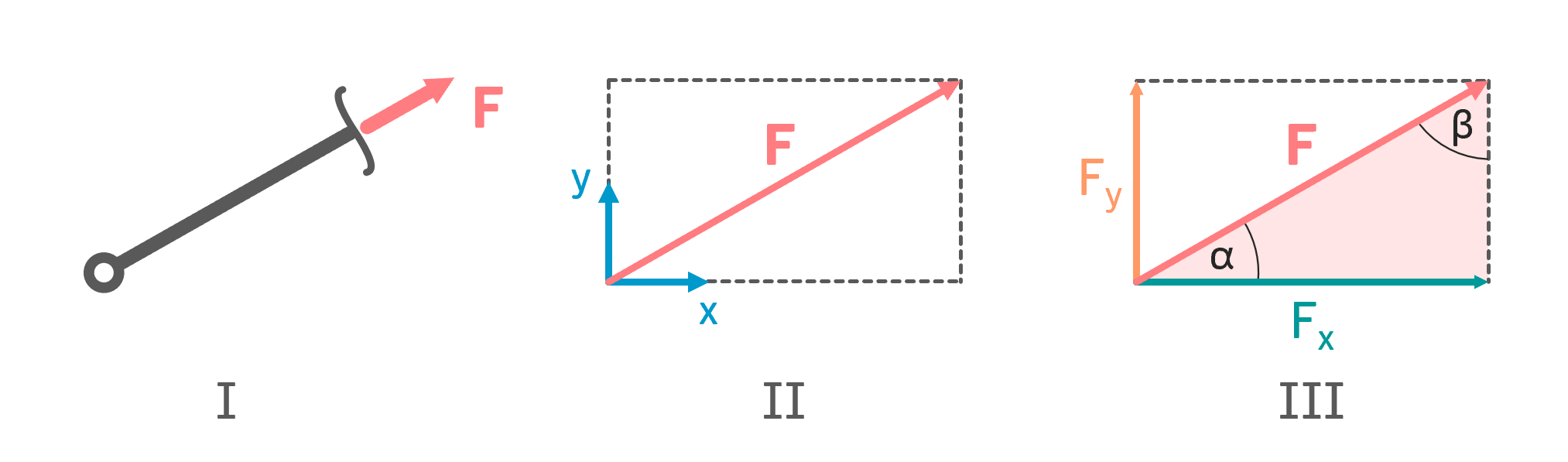
Nehmen wir eine beliebige Kraft, die in eine beliebigen Richtung zeigt. In diesem Fall ist es eine schräg wirkende Stabkraft (Bild I). Um die Kraft in ihre Komponenten zu zerlegen, deuten wir den x-Anteil und den y-Anteil der Kraft mit einer gestrichelten Linie an. Das Resultat ist ein angedeutetes Rechteck. Die horizontale Linie in diesem Rechteck entspricht dem x-Anteil und die vertikale Linie entspricht dem y-Anteil (Bild II). Rechts in Bild III ist das sogenannte Krafteck (oder auch Kräftedreieck) angedeutet: Ein rechtwinkliges Dreieck, bei dem die Hypotenuse der Gesamtkraft F entspricht und bei dem die Katheten (also die beiden kurzen Seiten des Dreiecks) die gesuchten x- und y-Komponenten repräsentieren.
Schritt 1: Krafteck zeichnen
Bleiben wir bei dem oben erwähnten Krafteck bzw. Kräftedreieck. Dieser ist nämlich der Ausgangspunkt der Kräftezerlegung. Hat man nämlich das Krafteck skizziert, ist die Kraft damit praktisch schon zerlegt. Das Kräftedreieck wird wie folgt skizziert.
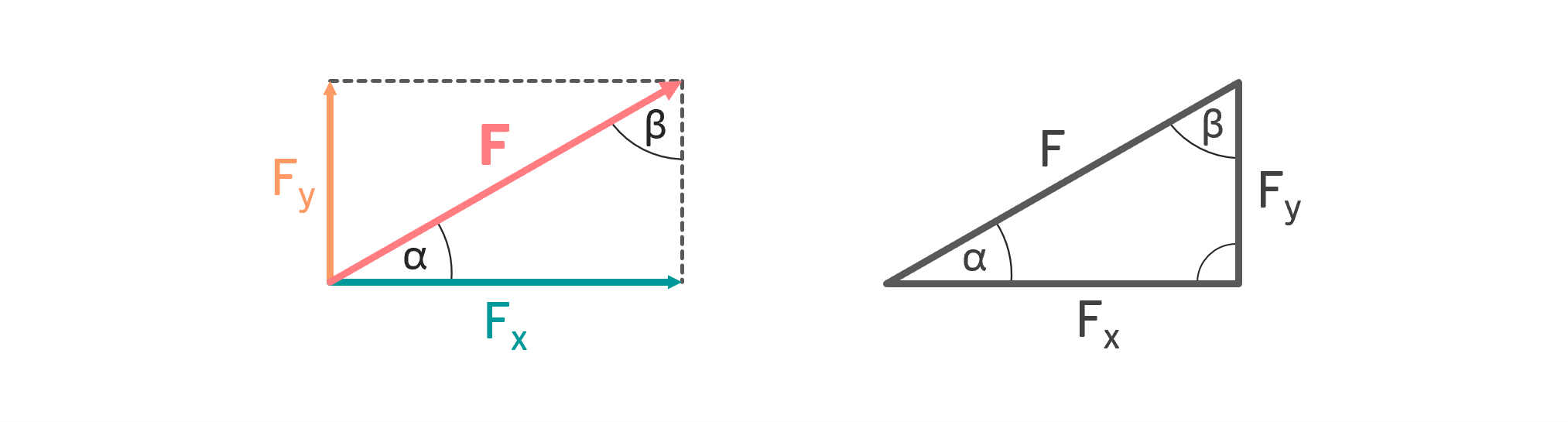
Schritt 2: Sinus und Cosinus und Pythagoras
In einem rechtwinkligen Dreieck darf man die Winkelbeziehungen anwenden. Außerdem gilt in einem rechtwinkligen Dreieck der Satz des Pythagoras. Für das vorliegende Krafteck bekommt man damit
$$cos(\alpha)=\frac{F_{x}}{F}$$ $$sin(\alpha)=\frac{F_{y}}{F}$$ $$tan(\alpha)=\frac{F_{y}}{F_{x}}$$ $$F^2=F_x^2+F_y^2$$
Man beachte, dass hier mit dem Winkel \( \alpha \) gearbeitet wurde. Wer mit dem gegenüberliegenden Winkel \( \beta \) arbeitet, hat eine andere An- und Gegenkathete als mit \( \alpha \).
Schritt 3: Kraft zerlegen
Um die Kräftezerlegung abzuschließen, müssen die Winkelbeziehungen aus dem vorherigen Schritt lediglich nach den gesuchten Kraftkomponenten umgestellt werden:
$$\Rightarrow F_x=F \cdot cos(\alpha)$$ $$\Rightarrow F_y=F \cdot sin(\alpha)$$
Diese beiden Gleichungen werden ab sofort zum täglichen Begleiter in der Technischen Mechanik oder gar im Studium. Es ist daher ratsam, den Umgang damit schnellstmöglich zu beherrschen.
Kräfteaddition
Man zerlegt Kräfte, damit man sie leichter zusammenrechnen kann. Hat man zwei Schräge Kräfte zerlegt, kann man ihre Komponenten problemlos addieren (bzw. voneinander abziehen).
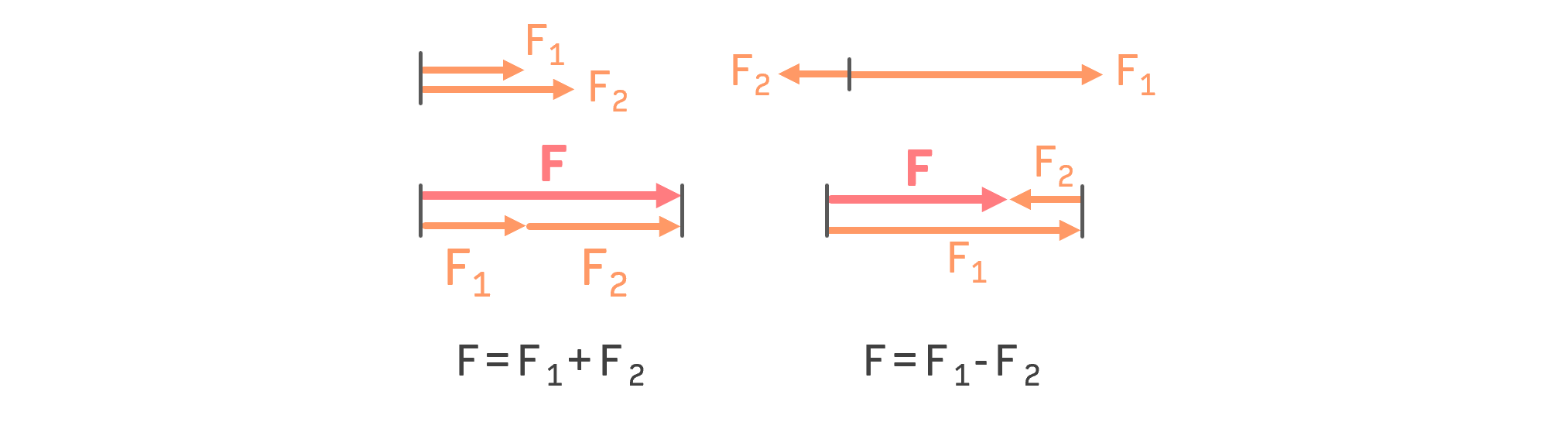
Je nachdem, ob die Kräfte in dieselbe Richtung zeigen oder nicht, rechnet man sie entweder zusammen, oder zieht sie voneinander ab:
$$F=F_1+F_2$$ $$F=F_1-F_2$$
Aufgabe: Kräfte zerlegen
Die dargestellte Vorrichtung wird zur Befestigung von Werbeschildern an Fassaden eingesetzt. Zu Berechnen ist die Stabkraft des schrägen Stabes 2 sowie die Komponenten der Stabkraft 2.
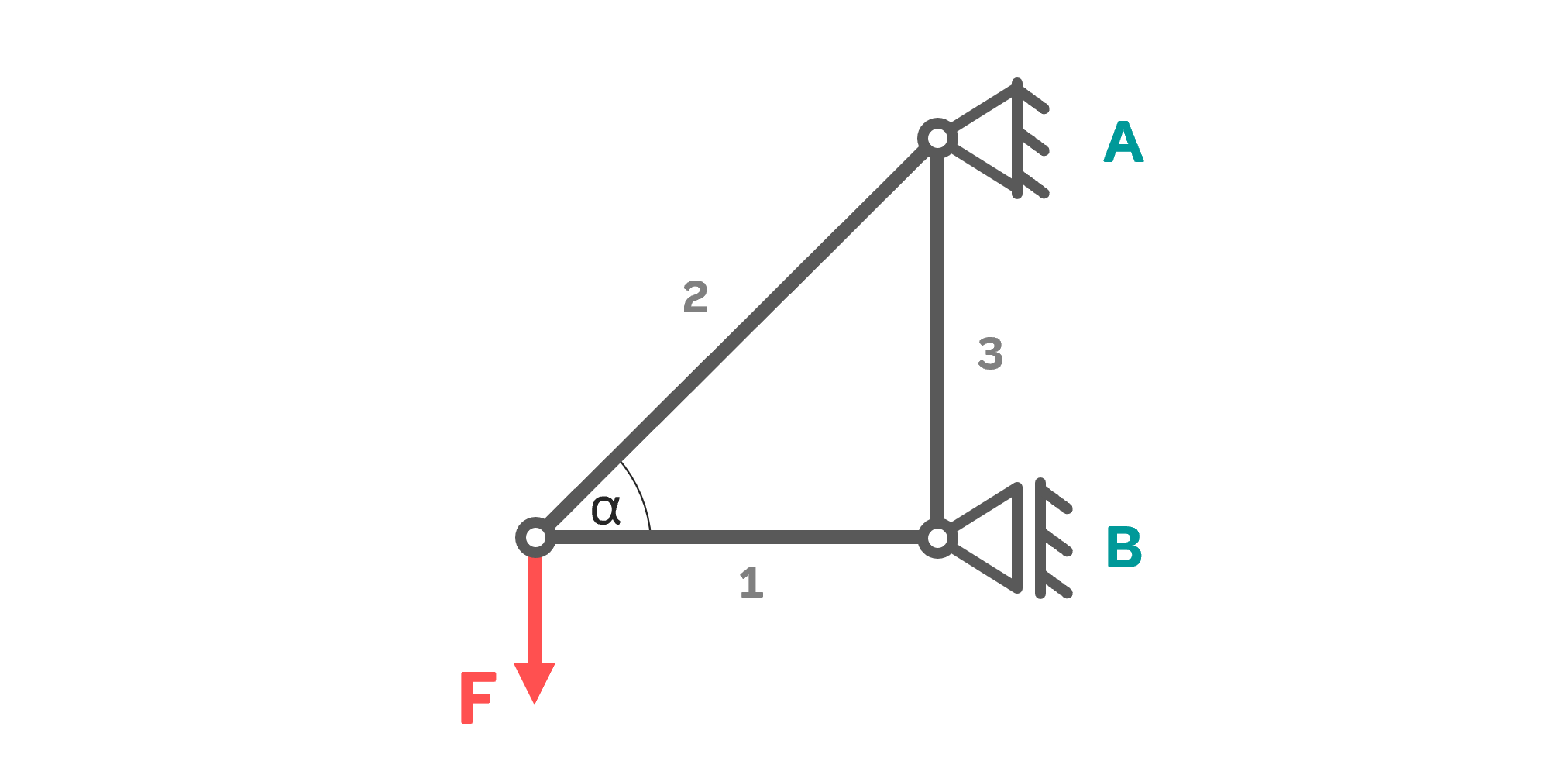
Gegeben: \( F=1000\,N,\,\alpha=40° \)
Lösung
Zuerst wird die gesuchte Stabkraft sichtbar gemacht. Das geschieht durch einen Freischnitt am Knotenpunkt, an dem sich der betroffene Stab befindet. Hier sieht man, dass insgesamt drei Kräfte am Knotenpunkt angreifen.
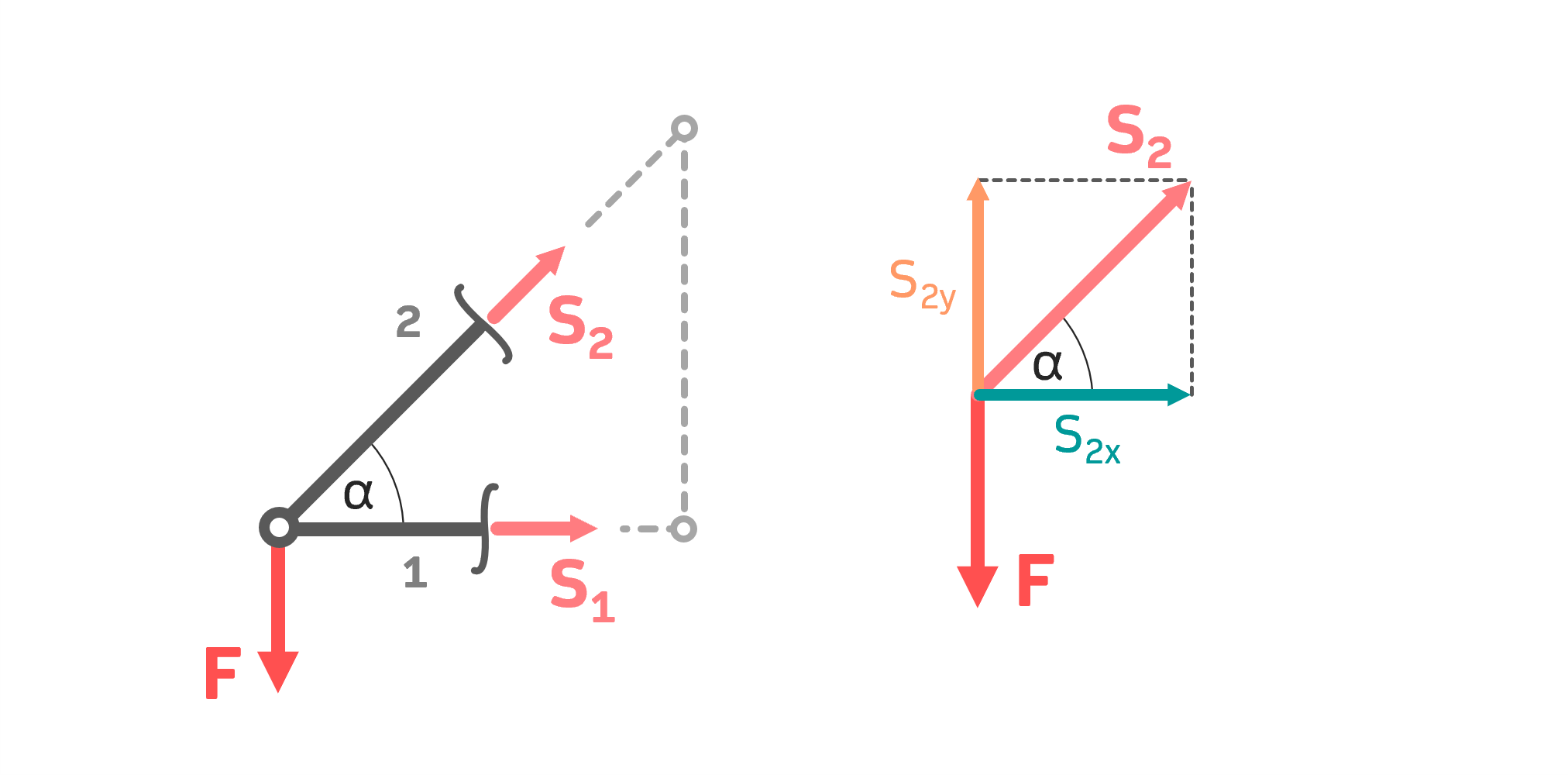
Stellt man das Kräftegleichgewicht in vertikaler Richtung auf, erhält man:
$$\sum F_V=0=S_{2y}-F$$ $$\Rightarrow S_{2y}=F=1000\,N$$
Die y-Komponente der Stabkraft 2 steht also im Gleichgewicht mit der Belastung durch das Werbeschild. Um von der y-Komponente auf die Gesamtstabkraft zu kommen, kann man den Sinus anwenden:
$$sin(\alpha)=\frac{S_{2y}}{S}$$
Stellt man nun nach der gesuchten Stabkraft um und setzt die Zahlenwerte ein, erhält man
$$\Rightarrow S=\frac{S_{2y}}{sin(\alpha)} \approx 1555,7\,N$$
Jetzt fehlt nur noch die x-Komponente der Stabkraft. Man kann sie entweder mit dem Cosinus bestimmen oder aber mit dem Pythagoras. Zu Übungszwecken werden beide Möglichkeiten vorgestellt:
$$cos(\alpha)=\frac{S_{2x}}{S}$$ $$S^2=S_{2x}^2+S_{2y}^2$$
Nun lassen sich beide Gleichungen nach der gesuchten x-Komponente umstellen:
$$\Rightarrow S_{2x}=S \cdot cos(\alpha) \approx 1191,8\,N$$ $$\Rightarrow S_{2x}=\sqrt{S_{2}^2-S_{2y}^2} \approx 1191,8\,N$$
Taschenrechner richtig einstellen
Denkt daran beim Umgang mit Sinus und Cosinus den Taschenrechner auf DEG zu stellen, um den Winkel richtig einzugeben (sofern der Winkel in Grad angegeben wird).
Zusammenfassung: Kräfte zerlegen
- Krafteck bzw. Kräftedreieck für die Kraft skizzieren
- Im rechtwinkligen Krafteck gelten die folgenden Beziehungen: $$cos(\alpha)=\frac{F_{x}}{F}$$ $$sin(\alpha)=\frac{F_{y}}{F}$$ $$tan(\alpha)=\frac{F_{y}}{F_{x}}$$ $$F^2=F_x^2+F_y^2$$
- Welche Gleichung wann einzusetzen ist, hängt von der jeweiligen Aufgabe ab.
Ausführliche Aufgabe zum Weiterüben: 2 Boote ziehen ein Schiff
FAQ: Kräftezerlegung
Wann Sinus und wann Cosinus?
Gute Frage! Das hängt zunächst davon ab, welche Seite des Dreiecks gesucht ist. Der Sinus liefert die Gegen- und der Cosinus die Ankathete. Damit ist es aber nicht getan, denn: Was die Gegen- und Ankathete ist, ist nicht fest vorgeschrieben. Gegenkathete bedeutet lediglich, dass sie gegenüber von dem betrachteten Winkel liegt. Ankathete bedeutet entsprechend, dass sie an dem Winkel anliegt. Ob man also Sinus oder Cosinus nehmen muss, hängt davon ab, welche Seite man sucht und wo sich der gegebene Winkel befindet.
Wie berechne ich die resultierende Kraft?
Ausgezeichnete Frage! Die resultierende Kraft kann in der Regel mit dem Satz des Pythagoras berechnet werden. Dafür benötigt man die Komponenten der Kraft:
$$F_{res}=\sqrt{F_x^2+F_y^2}$$
Wie addiert man zwei Kräfte?
Wenn die Kräfte parallel zueinander sind, kann man die Kräfte addieren, indem man sie einfach miteinander verrechnet. Zeigen die Kräfte hingegen in unterschiedliche Richtungen, dann müssen zuerst die Kräfte zerlegt werden. Hat man die x- und y-Komponenten der Kräfte, kann man sie einfach miteinander verrechnen.
Video: Kräftezerlegung beim Fachwerk
Die Kräftezerlegung taucht beispielsweise auf, wenn man Fachwerke berechnen (bzw. Stabkräfte berechnen) muss. Dieses Video zeigt anhand eines Fachwerks Schritt für Schritt, wie Kräfte zerlegt werden.
Verwandte Themen
Zentrales Kräftesystem
Flächenschwerpunkt: Überblick und Formeln
Oder zurück zur Themenübersicht: Technische Mechanik 1