Statische Bestimmtheit
Hier lernst du, mit der statischen Bestimmtheit umzugehen und was statisch bestimmte Systeme sind. Außerdem lernst du sowohl statisch überbestimmte Systeme als auch statisch unbestimmte Systeme kennen.
Wann ist etwas statisch bestimmt?
Kurzgesagt: Ein System ist dann statisch bestimmt gelagert, wenn sich die Lagerkräfte allein aus den drei Gleichgewichtsbedingungen berechnen lassen. Das System ist in diesem Fall „gut“ gelagert worden.
Beispiele für statische Bestimmtheit
Am leichtesten versteht man die statische Bestimmtheit, wenn man sich mit Fällen befasst, in denen das System nicht statisch bestimmt, also statisch unbestimmt ist.
Fall 1: Statisch unbestimmt
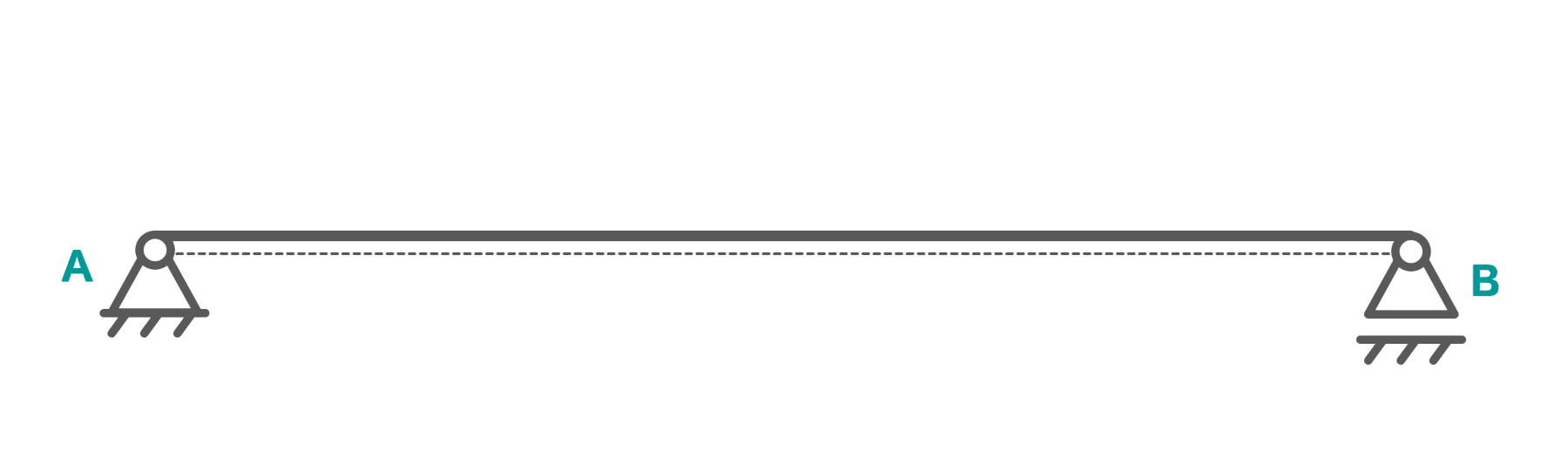
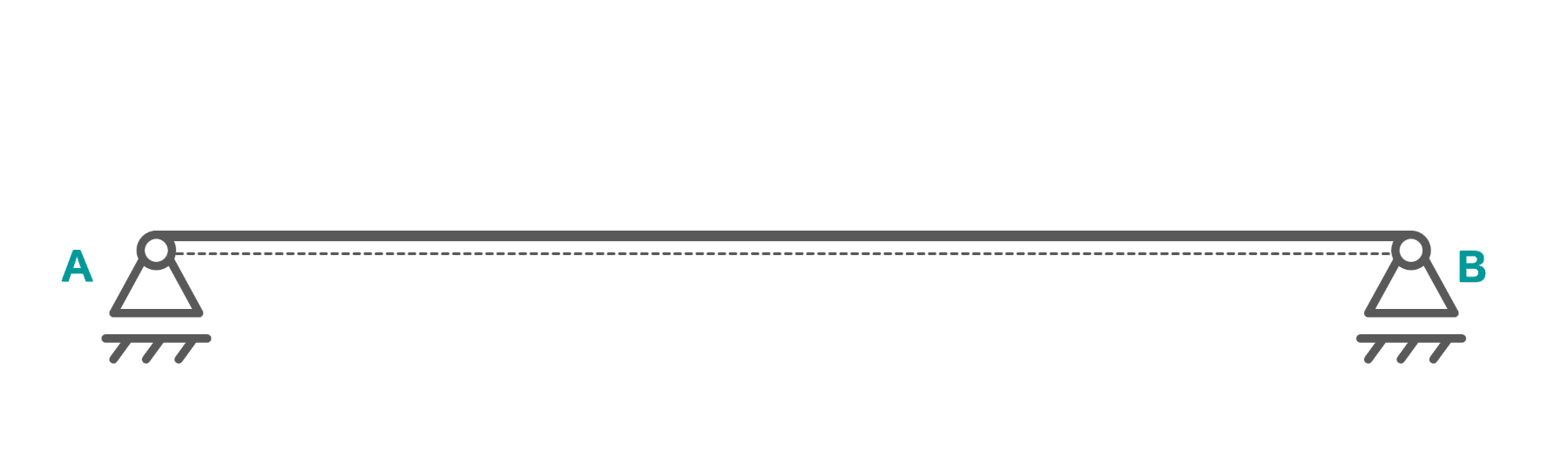
Die abgebildete Brücke stützt sich auf zwei Festlager und wird beim Übergang von Sommer zu Winter (und umgekerht) großen Temperaturschwankungen ausgesetzt. Der Balken ist statisch unbestimmt gelagert.
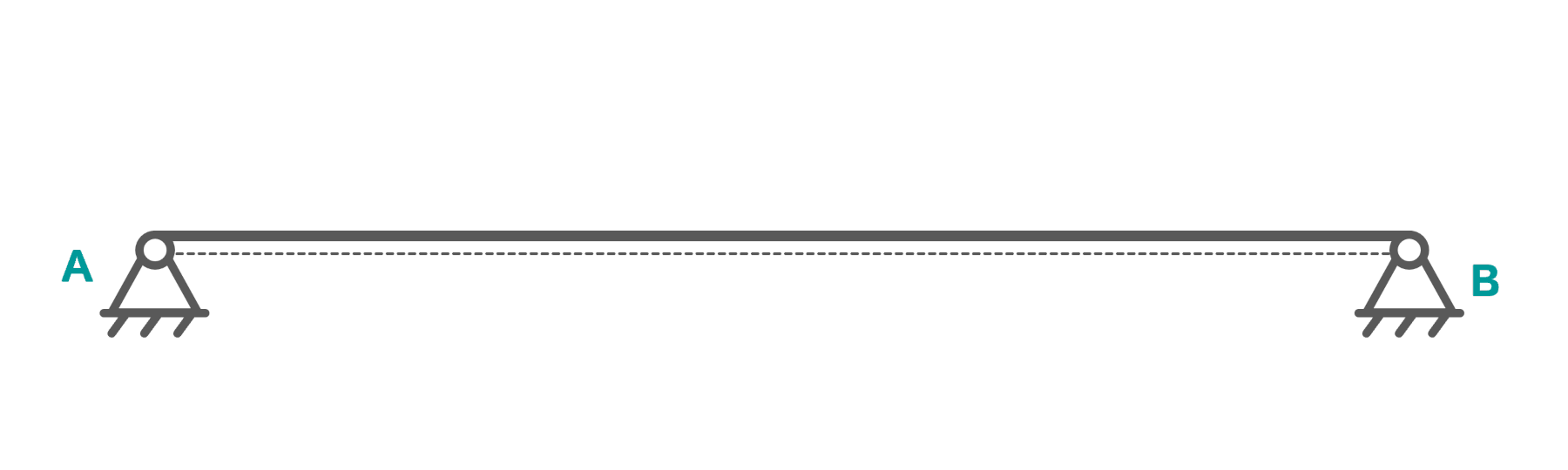
Auf den ersten Blick sieht das fest-fest-gelagerte System solide aus. Tatsächlich aber ist die gewählte Lagerung für diesen Einsatzzweck sehr gefährlich, denn: Die eingesetzten Werkstoffe dehnen sich bei Wärme und ziehen sich bei Kälte zusammen. Richtig gelesen: Eine Brücke bewegt sich um bis zu 30 Zentimeter zwischen der kalten und warmen Jahreszeit. Beobachten kann man das an der sogenannten Übergangskonstruktion.
Übergangskonstruktion

Bild: Pagvelius, CC BY-SA 4.0, via Wikimedia Commons
An der Übergangskonstruktion kann man die Dehnung einer Brücke beobachten: Wenn sich die Brücke im Sommer ausdehnt, dann wird der Spalt kleiner. Dementsprechend wird der Spalt im Winter kleiner, wenn sich die Brücke zusammenzieht. Um die Dehnung einer Brücke zu messen, haben die Ingenieure eine Skala unterhalb der Fahrbahn angebracht, an der die Längenänderung abgelesen werden kann.

Bild: Klaus-Dieter Keller, CC BY-SA 3.0, via Wikimedia Commons
Wieso ist ein statisch unbestimmtes System gefährlich?
Eine Brücke benötigt wie eingangs erwähnt Platz, um sich bei Hitze zu ausdehnen. Hat sie diesen Platz nicht, dann bauen sich im Inneren der Brücke Spannungen auf. Man kann sich hierzu einen Luftballon vorstellen, der in einer kleinen Schachtel steckt. Versucht man nun diesen Luftballon aufzublasen, dann drückt er von Innen gegen die Wand. Und zwar so lange, bis entweder der Luftballon Platz oder die Wand der Schachtel aufgrund des Drucks versagt.
Ein Festlager hat nun die Eigenschaft, dass es weder vertikale noch horizontale Verschiebungen zulässt. Installiert man nun an beiden Enden der Brücke jeweils ein Festlager, dann verhindert man damit die Dehnung der Brücke vollständig. Die Folge davon sind innere Spannungen, sobald sich die Brücke dehnen will. Wird nichts dagegen unternommen, kann das im schlimmsten Fall zum Versagen der Brücke führen.
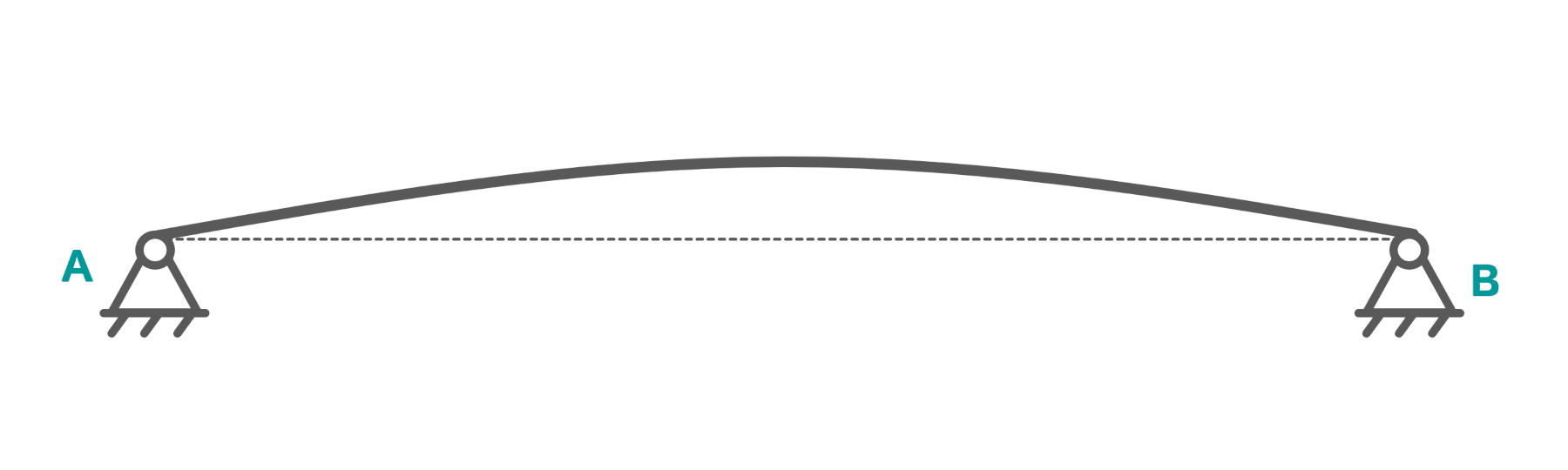
Aus diesem Grund darf ein Tragwerk nicht beidseitig festgelagert werden. Denn dann hätte man ein statisch unbestimmtes System.
Wie sollte man dann eine Brücke lagern?
Gute Frage! Wegen der Wärmedehnung einer Brücke muss ein freies „Atmen“ ermöglicht werden. Dazu nimmt man ein Festlager raus und ersetzt es durch ein Loslager.
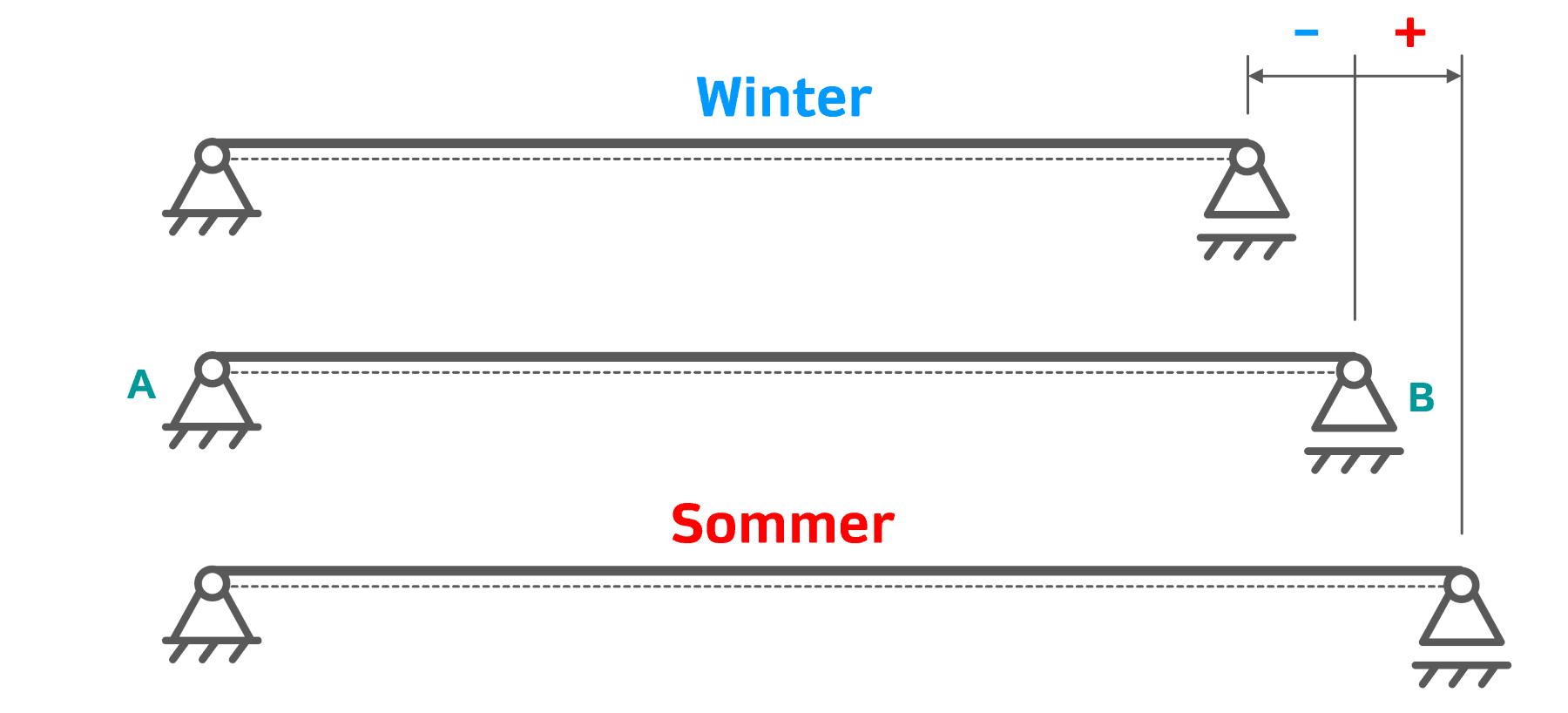
Das Loslager stützt die Brücke nach wie vor. Allerdings ermöglicht es jetzt ein horizontales Ausweichen. Damit kann sich die Brücke im Winter problemlos zusammenziehen und im Sommer ausdehnen. Die Brücke ist jetzt somit statisch bestimmt gelagert.
Muss man die Temperaturauswirkung nur bei Brücken berücksichtigen?
Ausgezeichnete Frage! Natürlich nicht. Grundsätzlich müssen alle ingenieurstechnisch relevanten Bauteile unter Last- und Temperatureinwirkungen nachgeben können. Insofern gilt es für jedes Bauteil, die Auswirkungen einer Temperaturänderung mitzuberücksichtigen.
Fall 2: Kinematisch unbestimmt
Im vorherigen Abschnitt haben wir glernt, dass es schlecht ist, wenn die Lagerung das System „zu sehr einschränkt“. In diesem Abschnitt lernen wir, dass es ebenfalls schlecht ist, wenn die Lagerung das System „nicht ausreichend einschränkt“. Nehmen wir als Beispiel diesen Balken, der sich auf drei Loslager stützt.
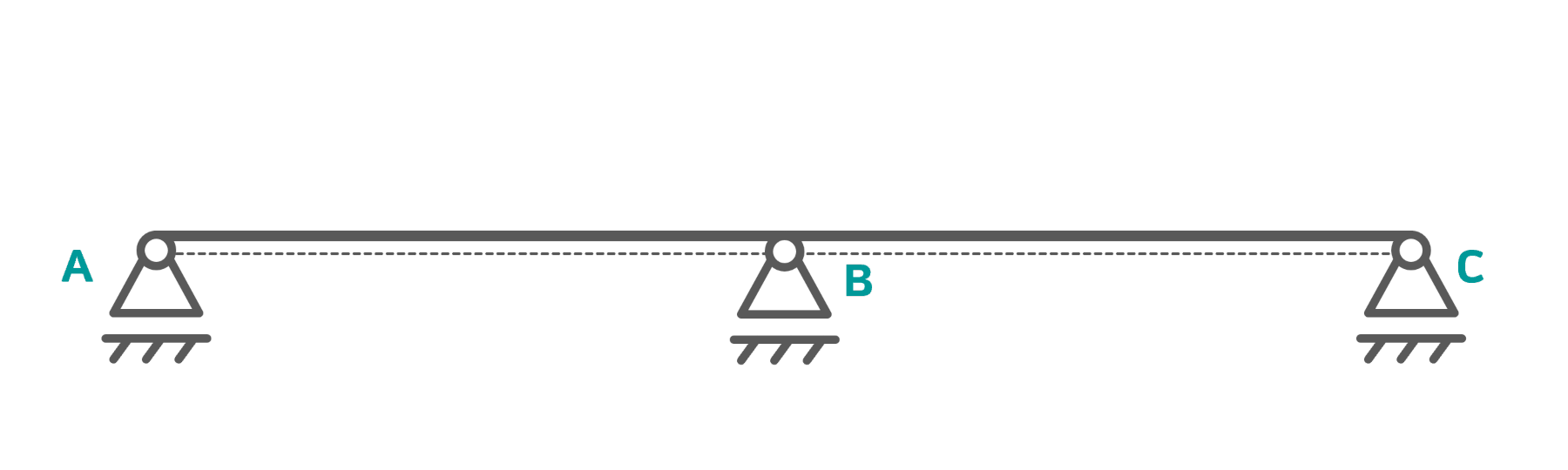
Man erkennt hier leicht, dass sich das System horizontal hin- und herbewegen kann. Sobald also eine horizontale Kraft bzw. eine schräge Kraft einwirkt, können die drei Loslager keinen Widerstand leisten und der Balken weicht zur Seite aus. Ein Einkaufswagen wäre (mehr oder weniger) auf diese Art richtig gelagert worden, schließlich soll ja ein Einkaufswagen hin- und herfahren. Ein Tragwerk aber, im Sinne der Statik, ist so definitiv nicht korrekt gelagert. Bewegliche Systeme werden in der Technischen Mechanik kinematisch unbestimmt genannt. Umgangssprachlich sagt der Mechaniker einfach nur beweglich.
Wie soll man dann hier den Balken richig lagern?
Wie schon im ersten Fall gilt: Der Balken muss zunächst an zwei Punkten gestützt werden. Und zusätzlich muss ein Lager dafür sorgen, dass der sich der Balken seitlich nicht komplett bewegen kann. Diese Anforderungen werden stets von der klassischen Fest-Los-Lagerung erfüllt. Es gibt allerdings auch andere Möglichkeiten, Balken zu lagern. Dazu aber später mehr.
Fall 3: Statisch bestimmt
Im Prinzip konnte man dank der vorherigen Beispiele bereits ein kleines Bauchgefühl entwickeln, welche Lagerungen grundsätzlich „gut“ und welche „schlecht“ sind. Die klassische Fest-Los-Lagerung bewährt sich als „gute“ Lagerung eines Balkens.

Wieso ist die Fest-Los-Lagerung eine gute Lagerung?
Gute Frage! Ein Balken ist zunächst der Oberbegriff für schlanke und lange Tragwerke, wie Brücken beispielsweise. Solche Brücken müssen nicht nur eine tragfähige Fahrbahn haben, sondern auch richtig gelagert sein. Ohne die richtige Lagerung ist eine tragfähige Fahrbahn nutzlos (und umgekehrt genauso). Die Fest-Los-Lagerung tut zunächst das Wichtigste: Sie stützt die Brücke an beiden Enden von unten. Außerdem sorgt das Festlager dafür, dass die Brücke nicht von ihrer vorgesehenen Einbaulage abweicht, sobald horizontale Kräfte einwirken. Darüber hinaus: Das Loslager ermöglicht der Brücke zeitgleich das oben erwähnte „Atmen“, also die freie Dehnung bei Temperaturänderung. Das sind die wichtigsten Anforderungen an einer Lagerung und die klassische Fest-Los-Lagerung erfüllt ebendiese Anforderungen. Daher ist ein fest-los-gelagerter Balken gut gelagert.
Gut gelagert = statisch bestimmt?
Im Rahmen der Lehrveranstaltungen Technische Mechanik 1-3 gilt: Ja, statisch bestimmt heißt „gut“ gelagert! Im Allgemeinen und vor allem in der Ingenieurspraxis gilt: Gut gelagert ist nicht immer statisch bestimmt gelagert! Allerdings haben solche Sonderfälle im Moment (noch) keine Bedeutung. Wir können uns also erstmal merken: Ein statisch bestimmt gelagerter Balken ist „gut“ gelagert. Statisch unbestimmt und kinematisch unbestimmt gelagerte Systeme sind „schlecht“ gelagert. Man kann die statische Bestimmtheit übrigens auch präziser angeben, sodass wir nicht auf die Adjektive „gut“ und „schlecht“ zurückgreifen müssen, um zu sagen, ob eine Brücke korrekt gelagert ist.
Statische Bestimmtheit Formel
Wir haben anhand von Beispielen gelernt, dass statisch bestimmt gelagerte Systeme „gut“ gelagert sind. In diesem Abschnitt lernen wir die Formel kennen, mit der man die statische Bestimmtheit eines Systems überprüfen kann.
$$f=3\,n-(r+v)$$
Jeder Körper hat in der Ebene drei Freiheitsgrade: Die beiden translatorischen Bewegungen (also die Geradeausbewegungen) in x- und y-Richtung und eine Rotation. Besteht das System aus zwei \( n=2 \) Körpern, dann hat es dementsprechend \( 3 \cdot 2 \) Freiheitsgrade. Diese \( 3n \) Freiheitsgrade werden von den Lagerreaktionen \( r \) und Gelenkreaktionen \( v \) „neutralisiert“. Ist ein System statisch bestimmt, dann gibt es genausoviele Lager- und Gelenkreaktionen wie es Freiheitsgrade gibt. In diesem Fall ist \( f=0 \).
Statisch unbestimmte Systeme
Für \( f<0 \) ist das System statisch unbestimmt. Die Zahl der Lagerreaktionen ist größer als die Anzahl der Freiheitsgrade. Die Lagerreaktionen lassen sich somit nicht alleine aus den Gleichgewichtsbedingungen bestimmen.
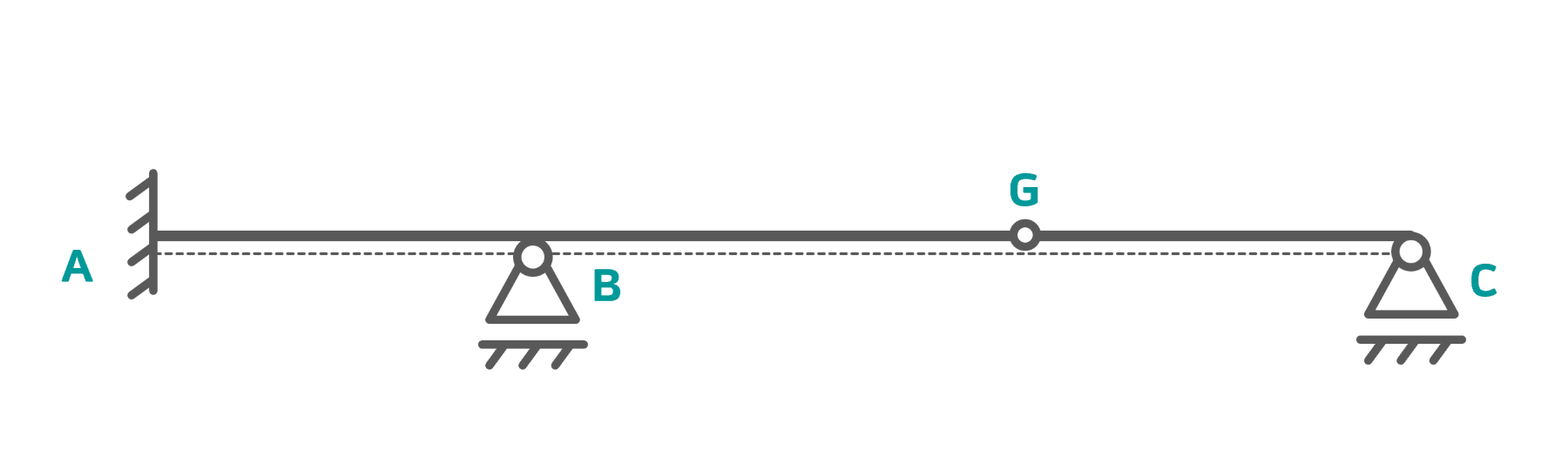
Das abgebildete System hat \( 3 \cdot 2 \) Freiheitsgrade, \( r=3+1+1 \) Lagerreaktionen und \( v=2 \) Gelenkreaktionen.
Setzt man das in die Formel ein, erhält man $$ f=3 \cdot 2 -(5+2) = -1 \neq 0$$
Wegen \( f=-1 \) ist das System 1-fach statisch überbestimmt. Zwar lassen sich die Lagerkräfte nicht mehr alleine mit den Gleichgewichtsbedingungen bestimmen, aber das System ist dennoch statisch brauchbar. Statisch unbestimmte Systeme sind nebenbei bemerkt Bestandteil der Festigkeitslehre und werden in der Veranstaltung Technische Mechanik 2 behandelt. Übrigens: Beim dargestellten System kann man das Loslager B entfernen, um das System statisch bestimmt zu machen.
Kinematisch unbestimmte Systeme
Für \( f>0 \) ist das System kinematisch unbestimmt. Die Zahl der Lagerreaktionen ist kleiner als die Anzahl der Freiheitsgrade. Es gibt daher nicht genug Lagerreaktionen, um das System vor ungewollten Bewegungen zu schützen. In diesem Fall würden beide Loslager seitlich nachgeben, wenn horizontale Kräfte einwirken.
Das abgebildete System hat \( 3 \cdot 1 \) Freiheitsgrade, \( r=1+1 \) Lagerreaktionen und \( v=0 \) Gelenkreaktionen.
Setzt man das in die Formel ein, erhält man $$ f=3 \cdot 1 -(2+0) = 1 \neq 0$$
Bewegen sich Systeme oder Teile eines Systems, spricht man von kinematisch unbestimmten Systemen. Solche Systeme sind statisch vollkommen unbrauchbar.
Statisch bestimmte Systeme
Bei statisch bestimmten Systemen ist stets \( f=0 \). Das bedeutet, dass alle Freiheitsgrade des Systems entzogen werden.

Ein fest-los-gelagerter Balken besitzt drei Freiheitsgrade, ein zweiwertiges Festlager und ein einwertiges Loslager, die dem Balken die drei Freiheitsgrade entziehen. Das System hat somit keine Freiheitsgrade mehr übrig, da
$$ f=3 \cdot 1 -(3+0)=0 $$
Gibt es Ausnahmefälle?
Leider ja. Tatsächlich gibt es Systeme, die laut Formel statisch bestimmt aber trotzdem beweglich sind.
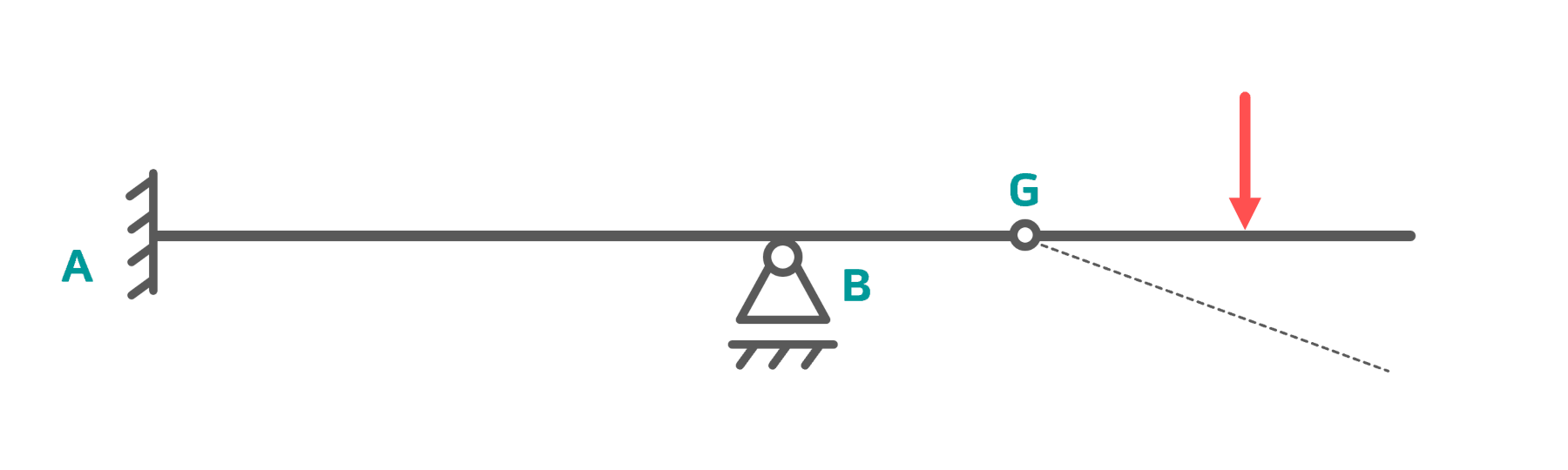
Für das abgebildete System ist $$ f=3 \cdot 2 -(4+2)=0 $$
Augenscheinlich ist \( f=0 \), wonach das System statisch bestimmt sein sollte. Allerdings sieht man hier auch, dass sich der rechte Abschnitt bei Lasteinwirkung absenken wird, womit das System kinematisch unbestimmt und somit unbrauchbar ist. Dieses Beispiel zeigt, dass die Formel alleine nicht ausreicht, um zu sagen, ob ein System statisch bestimmt ist oder nicht.
Zusammenfassung: Statische Bestimmtheit
Wir haben im vorherigen Abschnitt gelernt, dass es nicht ausreicht, die Formel alleine zu überprüfen. Ein System ist dann statisch bestimmt, wenn die Bedingung \( f=0 \) erfüllt ist und das System unbeweglich, also kinematisch bestimmt ist. Die Überprüfung der Formel gelingt immer und ist einfach umzusetzen. Bei der kinematischen Bestimmtheit muss man genauer hinsehen und das System verstehen. Nur wenn man das System verstanden hat, kann man sagen, ob es beweglich ist oder nicht.
- Formel für die statische Bestimmtheit: \(f=3\,n-(r+v)\)
- Statisch bestimmt: Wenn \( f=0 \) und System unbeweglich
- Kinematisch unbestimmt: \( f>0 \)
- Statisch unbestimmt: \( f<0 \)
\( n \) ist die Anzahl der Körper, \( r \) ist die Lagerwertigkeit (Anzahl der Lagerreaktionen) und \( v \) ist die Anzahl der Gelenkreaktionen. Ein System ist statisch bestimmt, wenn es genausoviele Lager- und Gelenkreaktionen gibt wie es Freiheitsgrade gibt. Die Lager- und Gelenkkräfte lassen sich allein aus den Gleichgewichtsbedingungen berechnen.
Video: Lagerkräfte berechnen
Passend zum Thema statische Bestimmtheit: Lagerkräfte berechnen (Rechenbeispiel).
Verwandte Themen
Kräftezerlegung
Lagerkräfte berechnen
Drehmoment berechnen
Zentrales Kräftesystem
Oder zurück zur Themenübersicht: Technische Mechanik 1