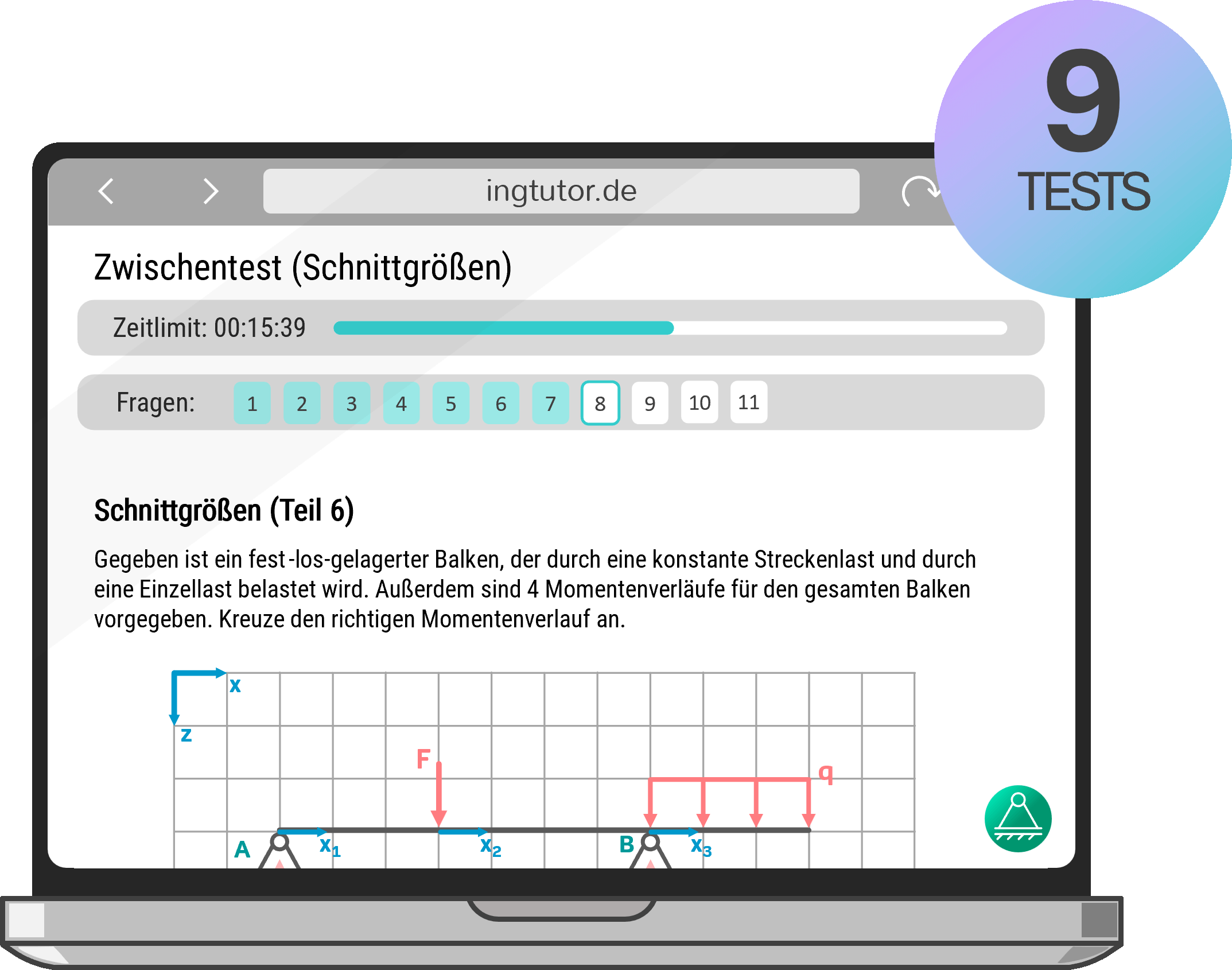
Zentrales Kräftesystem
Das zentrale Kräftesystem (auch zentrale Kräftegruppe) ist ein wesentlicher Bestandteil in der Technischen Mechanik 1. Greifen mehrere Kräfte auf einen Körper an und haben diese Kräfte einen gemeinsamen Angriffspunkt, dann spricht man vom zentralen Kräftesystem. Auf dieser Seite wird das zentrale Kräftesystem anhand einer Aufgabe beispielhaft erklärt.
Was versteht man unter einem zentralen Kräftesystem?
Ein zentrales Kräftesystem liegt vor, wenn sich mehrere Kräfte in einem Punkt schneiden oder wenn die Wirkungslinien der Kräfte sich in einem Punkt schneiden.
Aufgabe: Zentrales Kräftesystem
Zwei Schlepperschiffe ziehen mit den Kräften \( F_1,\:F_2 \) sowie den Richtungen \( \alpha,\: \beta \) ein großes Schiff. Zu berechnen ist die resultierende Kraft \( F_{res} \) und die Richtung \( \varphi \) der Resultierenden.
Gegeben: \( F_1=500\,kN,\;F_2=400\,kN,\;\alpha=30°,\;\beta=20° \)
Lösung
Schritt 0: Vorüberlegung
Man erkennt in der folgenden Abbildung gut, dass es sich um ein zentrales Kräftesystem (bzw. zentrale Kräftegruppe) handelt. Denn: Die beiden Kräfte \( F_1,\:F_2 \) haben in der Schleppöse (das ist dort, wo die Seile befestigt sind) einen gemeinsamen Angriffspunkt. Das bedeutet: Die Kräfte (bzw. die Wirkungslinien der Kräfte) schneiden sich dort. Sobald man dies erkennt, kann man mit dem nächsten Schritt weitermachen.
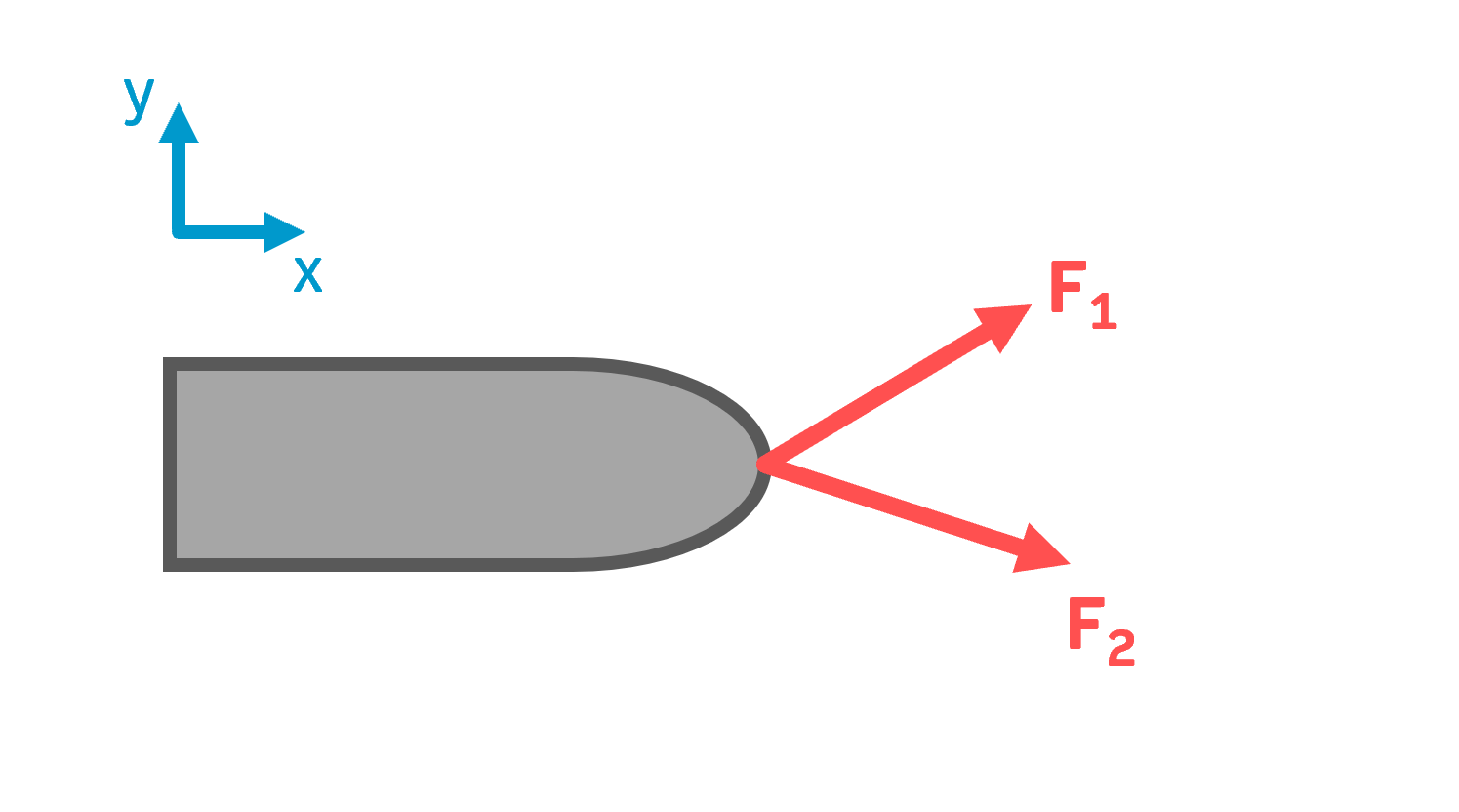
Schritt 1: Kräftezerlegung
Um die resultierende Kraft in einem zentralen Kräftesystem zu bestimmen, muss man zunächst die Kräfte zerlegen. Jede Kraft in der zentralen Kräftegruppe muss in einem x- und in einem y-Anteil zerlegt werden. Für die Kräftezerlegung wird zunächst die x- und y-Komponente der Kraft skizziert (siehe Bild). Wichtig ist dabei, dass die Winkel \( \alpha,\: \beta \) an der richtigen Stelle im Krafteck eingetragen werden.
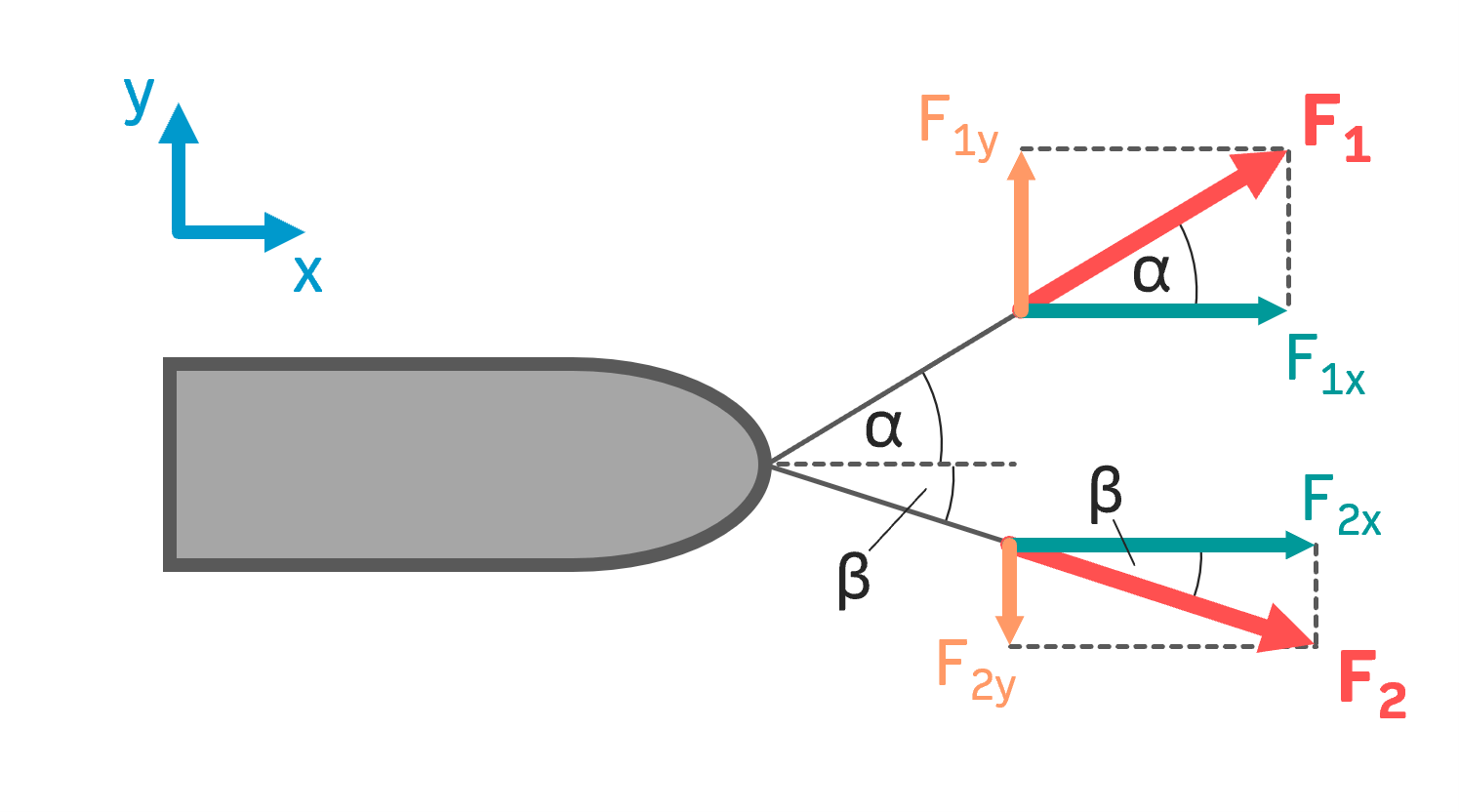
Sinus und Cosinus im Krafteck
Ist das Krafteck für die Kräfte \( F_1,\:F_2 \) gezeichnet worden, kann man mit dem Sinus und Cosinus die Kräfte wie folgt zerlegen:
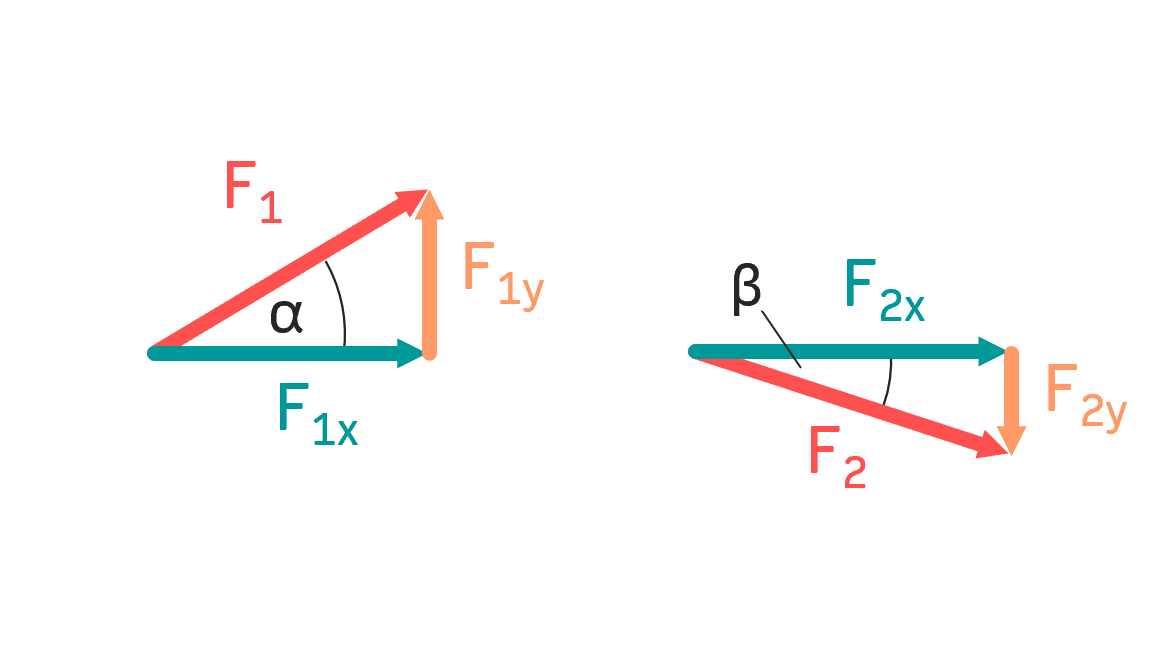$$cos(\alpha)=\frac{F_{1x}}{F_1}\:\Rightarrow F_{1x}=F_1 \cdot cos(\alpha)$$ $$sin(\alpha)=\frac{F_{1y}}{F_1}\:\Rightarrow F_{1y}=F_1 \cdot sin(\alpha)$$
$$cos(\beta)=\frac{F_{2x}}{F_2}\:\Rightarrow F_{2x}=F_2 \cdot cos(\beta)$$ $$sin(\beta)=\frac{F_{2y}}{F_2}\:\Rightarrow F_{2y}=F_2 \cdot sin(\beta)$$
Setzen wir die anfangs gegebenen Werte ein, erhalten wir:
$$F_{1x} \approx 433,0\:kN$$ $$F_{1y} = 250,0\:kN$$
$$F_{2x} \approx 375,9\:kN$$ $$F_{2y} = 136,8\:kN$$
Das Thema Kräftezerlegung wird hier separat erklärt: Kräftezerlegung (Grundlagen)
Schritt 2: Resultierende Kraft berechnen
Um die Resultierende \( F_{res} \) zu erhalten, müssen zunächst die zerlegten Kräfte jeweils zusammengerechnet werden. Man beachte hier, dass die vertikale Kraft \( F_{2y} \) nach unten zeigt und daher negativ zu berücksichtigen ist. Für die x- und y-Komponente der resultierenden Kraft gilt nämlich:
$$F_{res,x}=\sum F_{x,i}=F_{1x}+F_{2x} \approx 808,9\:kN$$ $$F_{res,y}=\sum F_{y,i}=F_{1y}-F_{2y}=113,2\:kN$$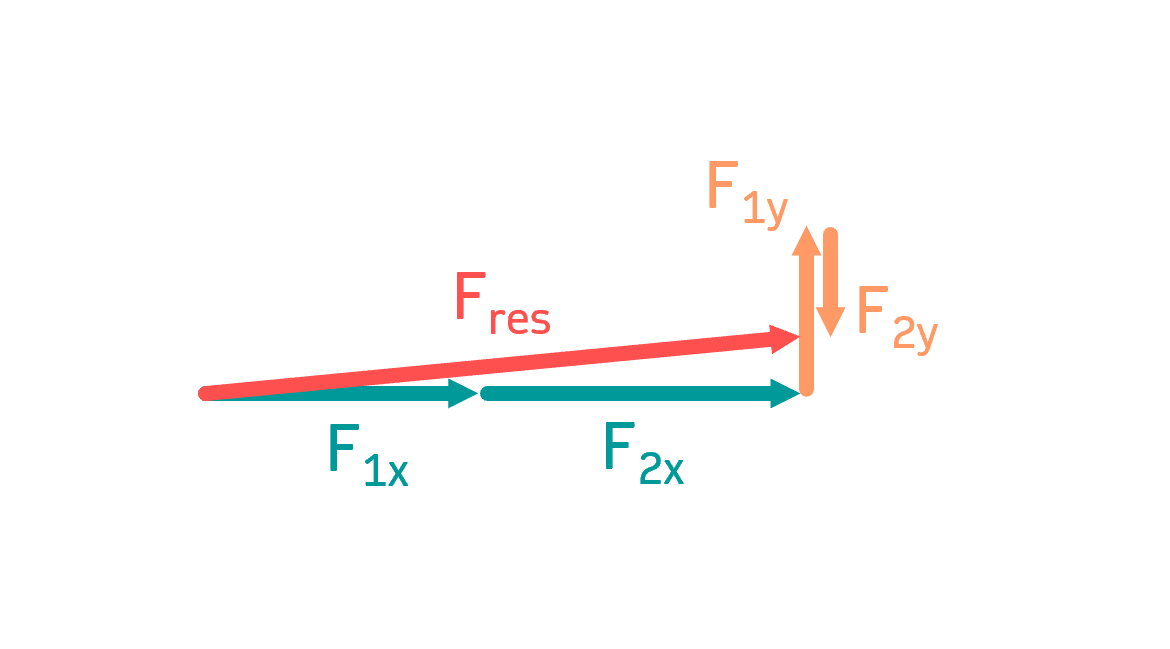
Pythagoras und Tangens im Krafteck
Die Komponenten \( F_{res,x} \) und \( F_{res,y} \) der resultierenden Kraft sind nun bekannt. Da die x- und y-Anteile der Resultiereden senkrecht aufeinander stehen, bilden sie ein rechtwinkliges Dreieck (Krafteck). Jetzt lässt sich die resultierende Kraft problemlos mit dem Satz des Pythagoras bestimmen. Die Richtung kann mit dem Tangens ermittelt werden:
$$F_{res}^2=F_{res,x}^2+F_{res,y}^2$$ $$\Rightarrow F_{res}=\sqrt{F_{res,x}^2+F_{res,y}^2} \approx 816,8\:kN$$
$$tan(\varphi)=\frac{F_{res,y}}{F_{res,x}} \Rightarrow \varphi \approx 8°$$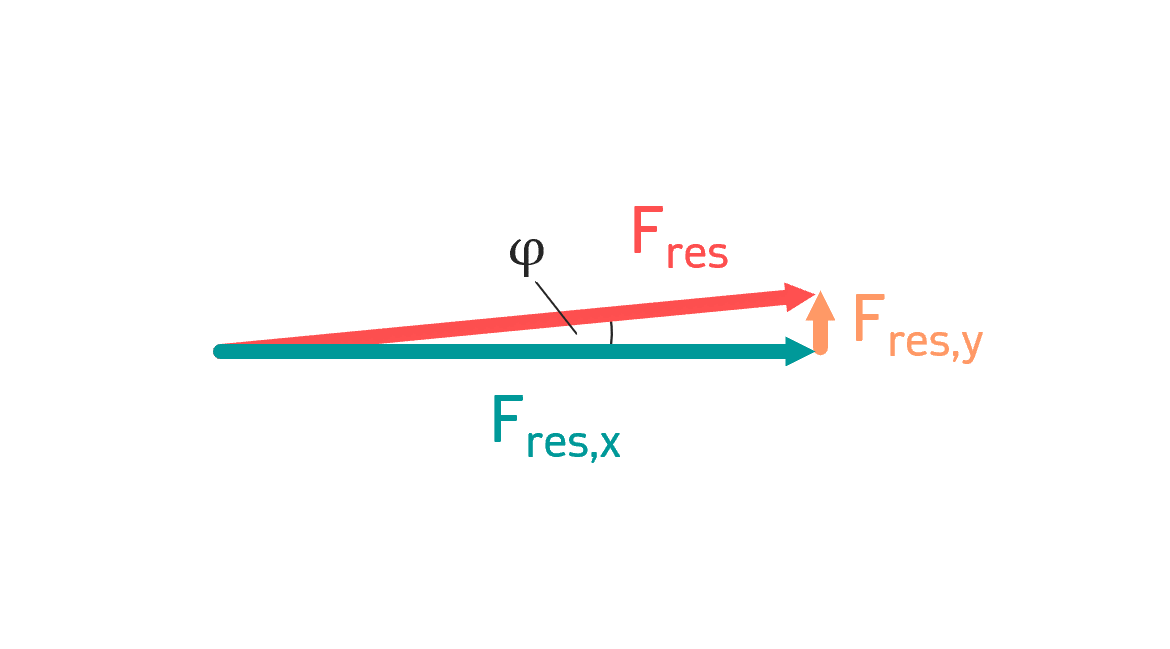
Taschenrechner richtig einstellen
Denkt daran an dieser Stelle den Taschenrechner auf DEG zu stellen, um den Winkel auszurechnen. Anderenfalls bekommt man das Ergebnis nicht in Grad sondern in Radiant.
Zusammenfassung: Zentrale Kräftegruppe
- Jede Kraft im zentralen Kräftesystem zerlegen (\( F_{1x},\:F_{1y} … \))
- x- und y-Komponente der resultierenden Kraft berechnen: $$ F_{res,x}=\Sigma F_{x,i}=F_{1x}+F_{2x}+… $$ $$ F_{res,y}=\Sigma F_{y,i}=F_{1y}+F_{2y}+… $$
- Resultierende Kraft mit dem Pythagoras und die Richtung mit dem Tangens berechnen: $$ F_{res}=\sqrt{F_{res,x}^2+F_{res,y}^2} $$ $$ tan(\varphi)=\frac{F_{res,y}}{F_{res,x}} $$
Ist das Ergebnis plausibel?
Die Richtung der resultierenden Kraft kann meistens grob abgeschätzt werden, ohne die Aufgabe dafür zu rechnen. Ein Blick auf die Aufgabenstellung genügt, um zu sagen, in welche Richtung das Schiff ungefähr gezogen wird. Diese Abschätzung kann dann mit dem berechneten Richtungswinkel \( \varphi \) verglichen werden, um zu sagen, ob das Ergebnis plausibel ist.
Vorzeichen beachten
Die Richtungen der zerlegten Kräfte sind für das Vorzeichen wichtig. Wenn Kräfte z.B. in die negative x-Richtung zeigen, dann gehen sie negativ in die Gleichungen ein.
Video zu dem Thema
Zentrale Kräftesysteme tauchen zum Beispiel auf, wenn man Fachwerke berechnen (bzw. Stabkräfte berechnen) muss. Dieses Video zeigt Schritt für Schritt, wie ein zentrales Kräftesystem berechnet wird anhand eines Fachwerks, wo die Stabkräfte berechnet werden.
Mit dem Laden des Videos akzeptieren Sie die Datenschutzerklärung von YouTube.
Mehr erfahren
Verwandte Themen
Kräftezerlegung: Theorie und Übungsbeispiel
Drehmoment berechnen
Streckenlast berechnen: Formeln und Überblick
Lagerkräfte berechnen
Oder zurück zur Themenübersicht: Technische Mechanik 1
