Start › Lernplattform › Technische Mechanik 1 › Haftung und Reibung › Seilreibung und Seilhaftung

Seilreibung und Seilhaftung

Hier erfährst du was die Seilreibung und Seilhaftung sind und wie man sie anhand der Euler-Eytelwein-Formel berechnet. Nach einer kurzen Einführung in die Theorie wird eine Rechenaufgabe zum Thema Seilreibung mit ausführlichem Lösungsweg berechnet.

Inhaltsverzeichnis

Was ist Seilreibung und Seilhaftung?
Wie berechnet man die Seilreibung?
1. Lastseite und Halteseite
2. Euler-Eytelwein-Formel
Aufgabe zur Seilreibung
Lösung
Zusammenfassung: Seilreibung
Verwandte Themen

Was ist Seilreibung und Seilhaftung?

Schlingt man ein Seil um einen Pfosten, dann entsteht zwischen dem Seil und der rauen Oberfläche des Pfostens Reibung, die wir hier Seilreibung bzw. Seilhaftung nennen. Die Reibung ist grundsätzlich so gerichtet, dass sie der Bewegung entgegenwirkt (weiterlesen: Grundlagen der Reibung). Dieses Prinzip gilt auch für die Seilreibung bzw. Seilhaftung. Man kann sich das zunutze machen, indem man beispielsweise eine schwere Masse mit der Gewichtskraft $ m \cdot g $ an einem Seil befestigt und dieses Seil um einen rauen Pfosten wickelt. Die Masse lässt sich nun mit einer (teils deutlich) geringeren Kraft $ F $ festhalten.

$$F < m \cdot g$$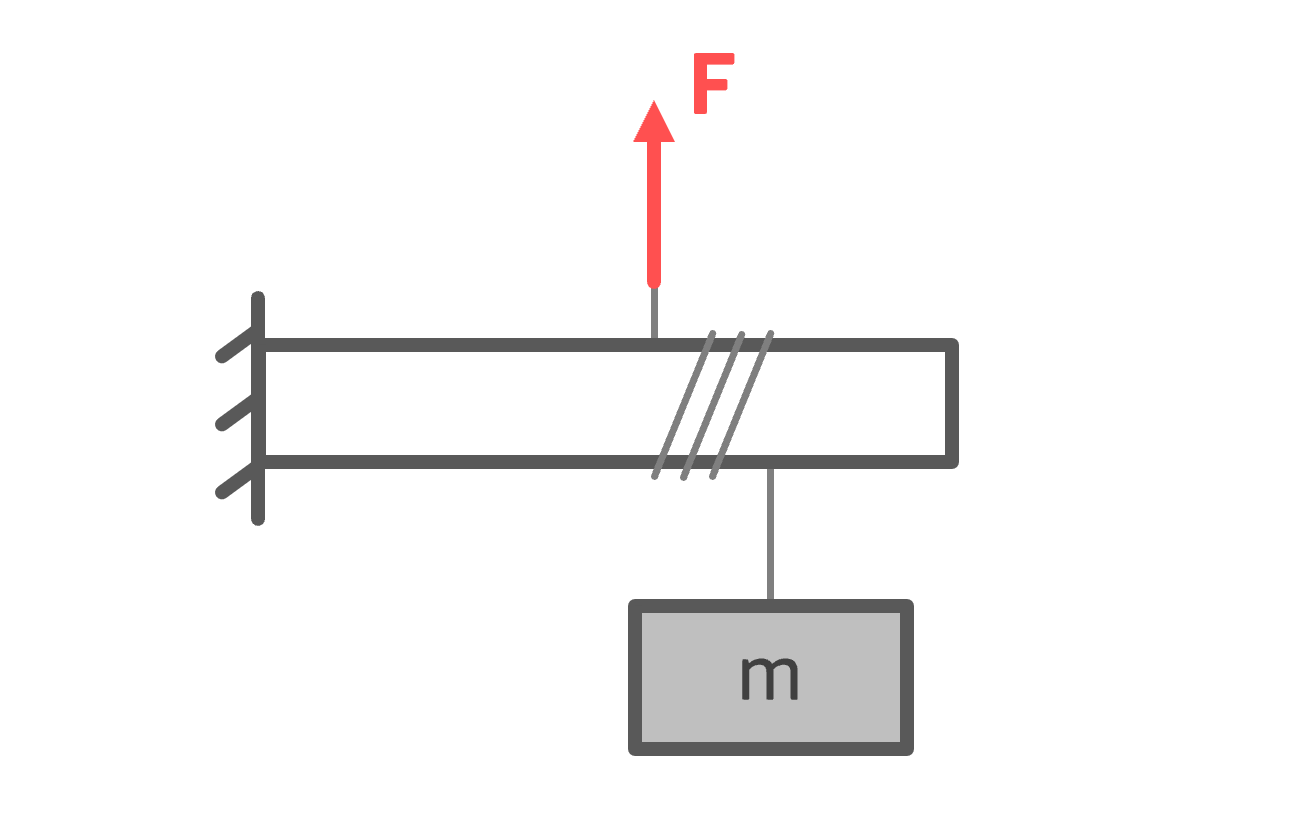 Seilreibung und Seilhaftung Beispiel INGTUTOR

Wieso ist die Haltekraft kleiner als die Last?

Gute Frage! Wie bereits erwähnt, wirkt die Reibung stets entgegengesetzt zur (möglichen) Bewegung. In diesem Fall versucht die schwere Masse nach unten zu fallen. Also wirkt die Reibung zwischen Seil und Pfosten so, dass das Herunterfallen erschwert wird. Das bedeutet, dass am anderen Ende des Seils nur noch eine kleine Kraft zum Halten erforderlich ist. Diesen Effekt findet man zum Beispiel bei Anlegepollern für Schiffe.

Seilreibung Anlegepoller INGTUTOR
Agnes Monkelbaan, CC BY-SA 4.0, via Wikimedia Commons

Wie berechnet man die Seilreibung?

Die Seilreibung bzw. Seilhaftung ist vom Umschlingungswinkel des Seils und vom Reibwert zwischen Seil und Poller abhängig. Bevor es allerdings an die Berechnung geht, sollten wichtige Grundbegriffe geklärt werden.

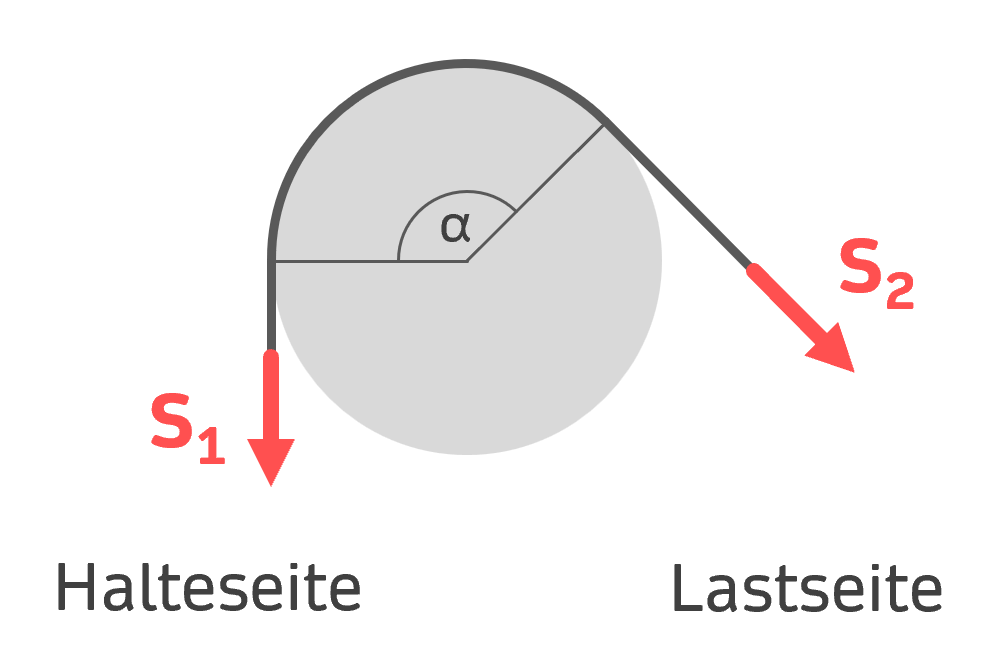
Lastseite Halteseite Seilreibung und Seilhaftung INGTUTOR

Lastseite und Halteseite

Es ist wichtig, dass man erkennt, auf welcher Seite die Last wirkt. In der Abbildung zieht die Last $ S_2 $ nämlich am Seil und verursacht somit eine (mögliche) Bewegung: Rutschen zur Lastseite. Wie wir bereits wissen, wirkt die Reibung der Bewegungsrichtung entgegen. Das bedeutet, dass die Seilreibung letzlich gegen die Last wirkt. Da die Seilreibung entgegengesetzt zur Last wirkt, unterstützt sie somit die andere Seite, nämlich die Halteseite. Die Halteseite ist dort, wo das Seil mithilfe der Haltekraft $ S_1 $ festgehalten wird. Da die Reibung die Halteseite unterstützt, ist stets eine geringere Haltekraft zum Festhalten der Last notwendig:

$$S_1 < S_2$$

Euler-Eytelwein-Formel

Bei der Seilreibung darf die Haltekraft $ S_1 $ kleiner sein als die eigentliche Last $ S_2 $, weil die Seilreibung unterstützend wirkt. Ist die Haltekraft aber zu gering, dominiert die Last und das Seil rutscht zur Lastseite hin. Daher ist der Mindestwert für die Haltekraft

$$S_{1,min}=S_2 \cdot e^{-\mu \cdot \alpha}$$

Dabei ist $ \alpha $ der Umschlingungswinkel (in rad) und $ \mu $ der Reibungskoeffizient. Ist die Haltekraft $ S_1 $ größer als die Last $ S_2 $, dann dominiert die Halteseite und es besteht die Gefahr des Rutschens zur Halteseite hin. In diesem Fall wirkt die Seilreibung nach wie vor gegen eine mögliche Bewegung und wirkt nun entgegengesetzt zur Halteseite. Erhöht man nach und nach die Haltekraft $ S_1 $, dann rutscht das Seil nicht sofort zur Halteseite hin. Denn: Die Reibung wirkt ja nun entgegengesetzt. Das bedeutet also, dass das Seil nicht rutscht, selbst wenn die Haltekraft $ S_1 $ größer ist als die Last $ S_2 $. Aber auch hier gibt es Grenzen: Ist die Haltekraft zu groß, dann dominiert sie und es kommt zum Rutschen zur Halteseite. Daher ist der Höchstwert für die Haltekraft

$$S_{1,max}=S_2 \cdot e^{\mu \cdot \alpha}$$

Die Haltekraft muss also in einem bestimmten Intervall, nämlich zwischen dem Mindest- und dem Höchstwert liegen, damit das Seil bzw. das System im Gleichgewicht ist. Liegt die Haltekraft unter dem Intervall, dann sie zu klein. In diesem Fall dominiert die Last und es kommt zum Rutschen zur Lastseite. Ist die Haltekraft hingegen über dem Intervall, dann ist sie zu groß. Hier dominiert dann die Haltekraft und es kommt zum Rutschen zur Halteseite. Das Intervall, in dem das System im Gleichgewicht ist, kann auch wie folgt formuliert werden:

$$S_2 \cdot e^{-\mu \cdot \alpha} \leq S_1 \leq S_2 \cdot e^{\mu \cdot \alpha}$$

Aufgabe zur Seilreibung

Ein Geländewagen mit defekten Bremsen schafft es nicht mehr, aus eigener Kraft den Hügel hochzufahren. Daher wird das Auto der Masse $ m $ mit Hilfe eines Seils festgehalten, bis ein Abschleppwagen zur Hilfe eilt. Am oberen Ende des Seils hält eine Person das Fahrzeug mit einer maximalen Zugkraft $ F $ fest. Selbstverständlich ist dies nur mit Hilfe der Seilreibung möglich. Anderenfalls wäre die menschliche Muskelkraft nicht ausreichend, um einen Geländewagen zu halten. Die Frage ist nun: Wie oft muss das Seil um den Baum mindestens gewickelt werden, damit die menschliche Zugkraft ausreichend ist, um den Wagen zu halten?

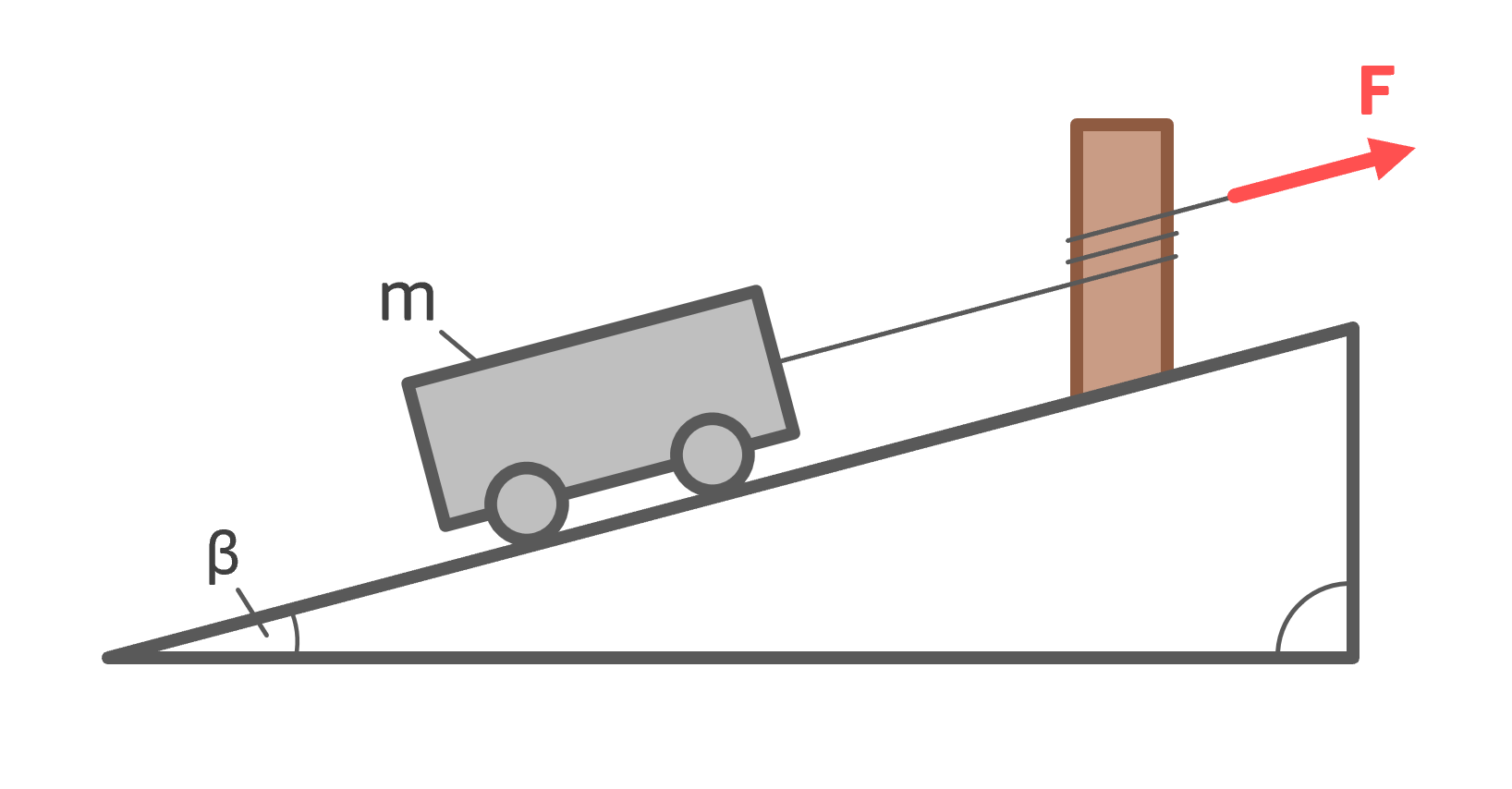
Seilreibung und Seilhaftung Aufgabe Euler Eytelwein Formel INGTUTOR

Gegeben: $ F=500\,N,\,m=2000\,kg,\,\beta=30°,\,g=9,81\,\frac{m}{s^2},\,\mu=0,3 $

Lösung

Mit Hilfe der Seilreibung ist es möglich, große Lasten mit einer geringen Haltekraft festzuhalten. Als erstes muss ermittelt werden, wie groß die Last auf der Lastseite ist. Dafür genügt ein Freischnitt der Masse (Freikörperbild).

Freischnitt

Zunächst wird das dargestellte x-y-Koordinatensystem eingeführt. Dabei ist die x-Achse parallel zur schiefen Ebene. Links ist das Freikörperbild der Masse zu sehen. Außerdem ist das Kräftedreieck der Gewichtskraft abgebildet.

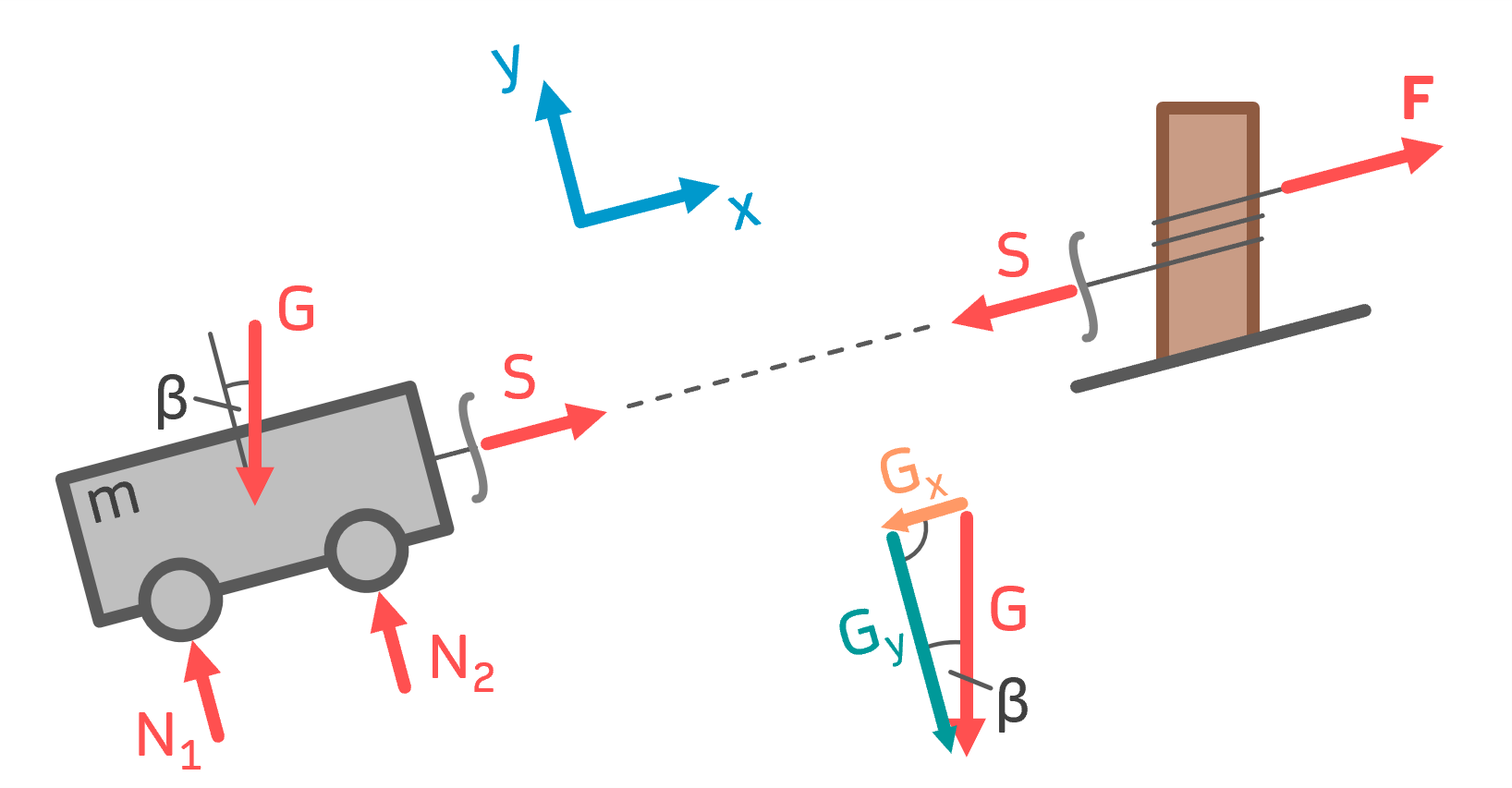
Seilreibung Seilhaftung Freischnitt Freikörperbild INGTUTOR

Gewichtskraft und Kräftezerlegung

Alle Kräfte im System zeigen vollständig in die x- oder y-Achse bis auf die Gewichtskraft $ G $. Diese kann mit dem gegebenen Koordinatensystem in ihre Komponenten zerlegt werden. Im Freischnitt wurde die Gewichtskraft bereits zeichnerisch zerlegt. Es gilt:

$$G=m \cdot g = 19620\,N$$ $$G_x=G \cdot sin(\beta)=9810\,N$$

Gleichgewichtsbedingung

Es ist zunächst die Kraft auf der Lastseite zu ermitteln. Das ist die Kraft, mit der das Auto am Seil zieht. Stellt man für den Geländewagen die Gleichgewichtsbedingung in x-Richtung auf, erhält man die gesuchte Kraft $ S $:

$$\sum F_x=0=S-G_x$$ $$\Rightarrow S=G_x=9810\,N$$

Umschlingungswinkel

Die Kraft auf der Halteseite $ F $ und die Kraft auf der Lastseite $ S $ sind bekannt. Mit Hilfe der Euler-Eytelwein-Formel

$$S_{1,min}=S_2 \cdot e^{-\mu \cdot \alpha}$$ kann der gesuchte Umschlingungswinkel ermittelt werden. Dazu setzen wir zunächst die bekannten Kräfte ein: $$F=S \cdot e^{-\mu \cdot \alpha}$$

Es ist zu ermitteln, wie oft das Seil um den Baum gewickelt werden muss. Daher muss nach dem Umschlingungswinkel $ \alpha $ umgestellt werden. Zuerst wird die Kraft $ S $ auf die linke Seite geholt:

$$\Rightarrow \frac{F}{S} = e^{-\mu \cdot \alpha}$$

Danach wird der Logarithmus angewandt, um die e-Funktion zu neutralisieren. Dadurch rutscht der Exponent runter, sodass man damit arbeiten kann.

$$\Rightarrow ln \left( \frac{F}{S} \right) = -\mu \cdot \alpha$$

Im letzten Schritt können wir ganz einfach nach $ \alpha $ umstellen:

$$\Rightarrow \alpha = -\frac{ln \left( \frac{F}{S} \right)}{\mu}$$

Setzt man nun die gegebenen Größen ein, erhält man für den Umschlingungswinkel:

$$\alpha \approx 9,92$$

Man darf nicht vergessen, dass bei der Seilreibung der Winkel in rad angegeben wird. Das bedeutet, dass eine volle Umdrehung am Kreis $ 2\pi $ entspricht. $ n $ Umdrehungen am Kreis sind dementsprechend

$$\alpha = 2\pi \cdot n$$

Die ursprüngliche Fragestellung war: Wie oft muss das Seil um den Baum gewickelt werden? Die Antwort erhalten wir, indem wir nach $ n $ umformen: $$\Rightarrow n = \frac{\alpha}{2\pi}$$ $$n \approx 1,58$$

Der Umschlingungswinkel ist in diesem Fall als Mindestwert zu verstehen und darf nicht unterschritten werden. Mit nur knapp 1,6 Wicklungen kann man mit reiner Muskelkraft und dank der Seilreibung einen Geländewagen davon abhalten, den Hang hinunter zu rollen. Zur Erinnerung: Die Haltekraft der Person beträgt 500 Newton, das sind umgerechnet etwas mehr als 50 Kilogramm. Die Kraft, mit der das Auto am Seil zieht, beträgt 9810 Newton. Das entspricht umgerechnet einer Tonne Last. Dieses Beispiel zeigt eindrucksvoll, wozu die Seilreibung also imstande ist.

Zusammenfassung: Seilreibung

Aufgaben zum Thema Seilreibung bzw. Seilhaftung erfordern ein genaues Verständnis über die Lastseite und über die Halteseite. Manchmal ist das nicht ganz leicht zu erkennen, wenn die Aufgabe umständlich formuliert ist. Um typische Seilreibungs-Aufgaben zu lösen, kann man folgende Punkte abarbeiten: