Prüfungsaufgabe: Lagerkräfte berechnen
Lagerkräfte berechnen: Hier wird eine ehemalige Prüfungsaufgabe zu Übungszwecken Schritt für Schritt berechnet. Dabei geht es um einen Balken mit Fest-Los-Lagerung und verschiedenen Belastungen: Dreieckslast, schräge Einzelkraft und Moment.
Was ist eine Lagerkraft?
Kräfte die ein Lager aufnehmen kann, werden Lagerkräfte oder Lagerreaktionen genannt. Man nennt sich Lagerreaktionen, weil sie auf äußere Belastungen reagieren.
Aufgabe: Lagerkräfte berechnen
Der abgebildete Balken mit der Länge \( 8a \) ist auf einer Fest-Los-Lagerung befestigt und wird mit der schrägen Kraft \( F \), der Dreieckslast (Streckenlast) mit Spitzenwert \( q_0 \) und dem Moment \( M \) belastet. Zu Berechnen sind die Lagerkräfte \( A_H,\:A_V,\:B_V \) des Systems.
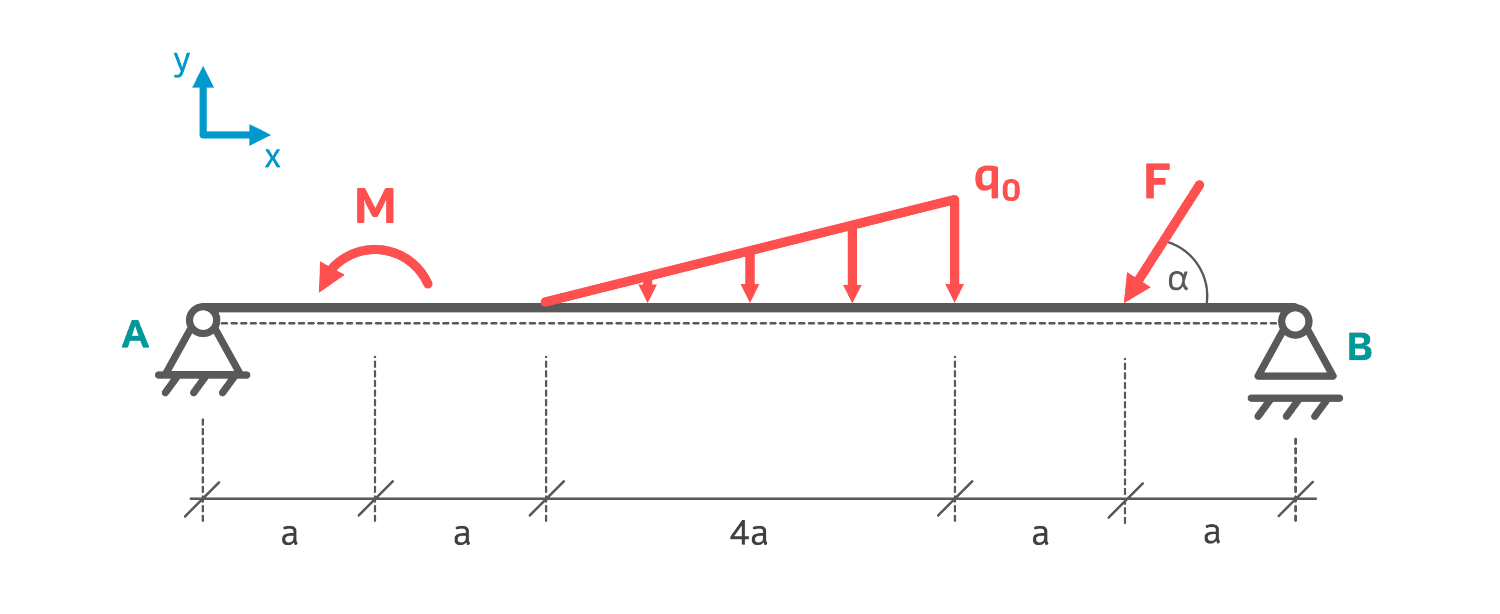
Gegeben: \( q_0=10\,\frac{kN}{m},\; F=15\,kN,\; M=25\,kNm,\; a=1\,m,\; \alpha=30° \)
Lösung
Schritt 1: Freischneiden
Das Freikörperbild bzw. der Freischnitt enthält neben den Lagerreaktionen \( A_H,\:A_V,\:B_V \) des Fest- und Loslagers auch die zerlegte Kraft \( F \) und die resultierende Kraft der Dreieckslast, auf die im Folgenden genauer eingegangen wird.
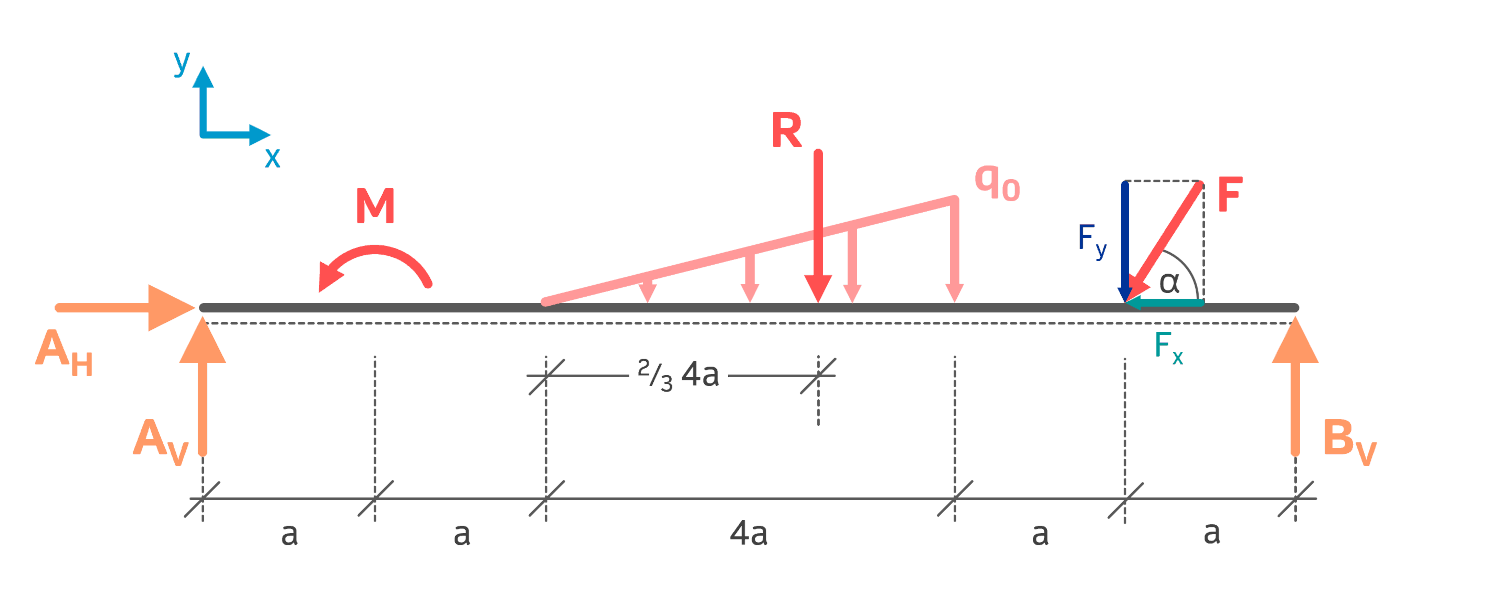
Dreieckslast
Alle relevanten Informationen über Streckenlasten kann man der Liste mit den wichtigsten Streckenlasten entnehmen. Dazu gehört in diesem Fall der Betrag der resultierenden Kraft sowie der Kraftangriffspunkt:
$$R=\frac{1}{2}\:q_0 \cdot 4a = 2\,q_0a=20\,kN$$ $$x_{S}=\frac{2}{3}\:4a=\frac{8}{3}a \approx 2,67\,m$$
Kräftezerlegung
Die Kräfte werden mit dem Krafteck und mit den Winkelbeziehungen zerlegt. Ausführliche Erklärung: Kräftezerlegung (Grundlagen). Für den oben gezeigten Freischnitt gilt:
$$F_x=F \cdot cos(\alpha) \approx 13\,kN$$ $$F_y=F \cdot sin(\alpha)=7,5\,kN$$
Drehmoment (Moment)
Das Drehmoment bzw. das Moment \( M \) kann einfach so in das Freikörperbild (Freischnitt) übernommen werden. Es wird im nächsten Schritt in der Momentengleichung bei den Gleichgewichtsbedingungen berücksichtigt.
Schritt 2: Gleichgewichtsbedingungen aufstellen
Summe aller Momente um Punkt A:
$$\sum M^A=0=B_V \cdot 8a-F_y \cdot 7a-R \cdot (2a+\frac{8}{3}a)+M$$ $$\Rightarrow B_V \cdot 8a=F_y \cdot 7a+R \cdot \frac{14}{3}a-M$$ $$\Rightarrow B_V = \frac{F_y \cdot 7a+R \cdot \frac{14}{3}a-M}{8a}$$ $$B_V \approx 15,1\,kN$$
Summe aller Kräfte in x-Richtung (Horizontalkräfte):
$$\sum F_H=0=A_H-F_x$$ $$\Rightarrow A_H=F_x \approx 13\,kN$$
Summe aller Kräfte in y-Richtung (Vertikalkräfte):
$$\sum F_V=0=A_V+B_V-F_y-R$$ $$\Rightarrow A_V=F_y+R-B_V \approx 12,4\,kN$$
Video zum Thema Lagerkräfte berechnen
In diesem Video wird erklärt, wie man Schritt für Schritt Lagerkräfte berechnen kann, wenn eine Kraft und eine Streckenlast den Balken belasten.
Mit dem Laden des Videos akzeptieren Sie die Datenschutzerklärung von YouTube.
Mehr erfahren
Zusammenfassung: Lagerkräfte berechnen
- Freikörperbild zeichen: Auflagerkräfte und Resultierende der Streckenlast einzeichnen, schräge Kräfte zerlegen
- Gleichgewichtsbedingungen aufstellen (\( \Sigma\:M,\:\Sigma F_x,\:\Sigma F_y \))
- Gleichgewichtsbedingungen nach den gesuchten Lagerkräften umstellen
Reihenfolge beachten
Die Summe der Momente als erstes aufstellen, weil hier nur eine Lagerkraft auftaucht. Das bedeutet, dass man diese Lagerkraft direkt erhält. Im Kräftegleichgewicht in y-Richtung hingegen stecken zwei unbekannte Lagerkräfte: \( A_V \) und \( B_V \). Diese können nicht direkt bestimmt werden.
Verwandte Themen
Statische Bestimmtheit
Resultierende der Streckenlast und Kraftangriffspunkt (Dreieckslast, Trapezlast, Gleichstreckenlast)
Schräge Kräfte zerlegen beim zentralen Kräftesystem
Kräftezerlegung: Theorie und Übungsbeispiel
Oder zurück zur Themenübersicht.
