Schnittgrößen berechnen
Hier erfährst du, wie du Schnittgrößen berechnen kannst. Dafür wird ein Balken mit einer Fest-Los-Lagerung betrachtet, auf dem die Kraft \( F \) wirkt. Anhand dieser Einführungsaufgabe werden die Schnittgrößen Schritt für Schritt berechnet. Neben einer ausführlichen Rechnung erfährst du auch, was für die Klausur wichtig ist.
Welche Schnittgrößen gibt es?
Es gibt drei Schnittgrößen: Die Normalkraft \( N \), die Querkraft \( Q \) und das Biegemoment \( M_b \). Schnittgrößen sind innere Kräfte des Balkens und werden durch einen Schnitt sichtbar gemacht. Die Schnittgrößen sind wichtig, um zu sagen, wie groß die Belastung in einem Bauteil ist.
Aufgabe: Schnittgrößen berechnen
Der abgebildete Balken der Länge \( L=10\,m \) ist fest-los-gelagert und wird mit der Kraft \( F=10\,kN \) vertikal belastet. Es sind die Schnittgrößen \( N(x),\:Q(x),\:M_b(x) \) des Balkens zu bestimmen.
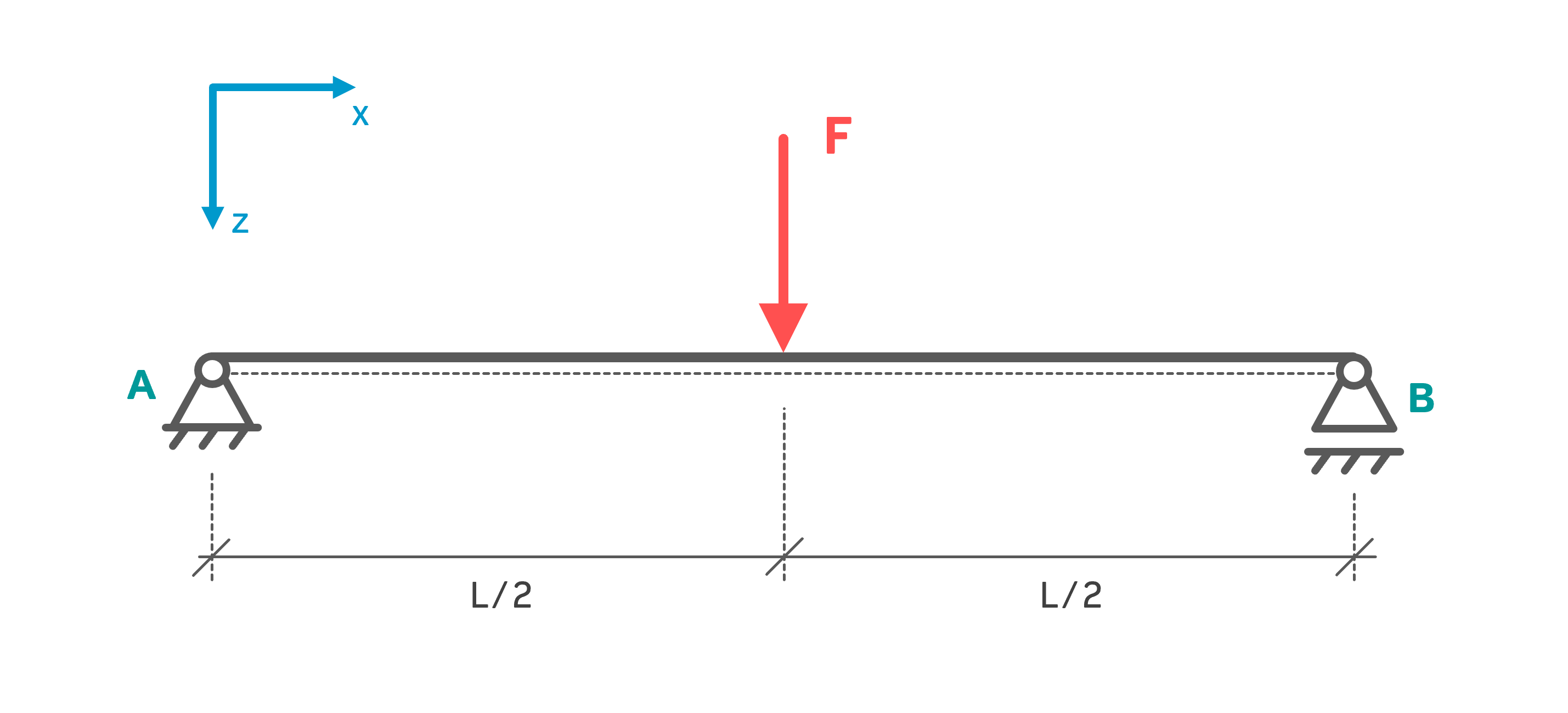
Gegeben: \( F=10\,kN,\; L=10\,m \)
Lösung
Schritt 1: Lagerkräfte berechnen
Bevor die Schnittgrößen berechnet werden können, müssen zuerst die Lagerkräfte berechnet werden. Zumindest in den meisten Fällen. Die Lagerkräfte dieses Systems wurden hier (Lagerkräfte berechnen) bereits berechnet. Schau dort gerne rein, wenn du mit den Lagerkräften Schwierigkeiten hast. Was die Schnittgrößen angeht, so können wir die Lagerkräfte nun als bekannt annehmen.
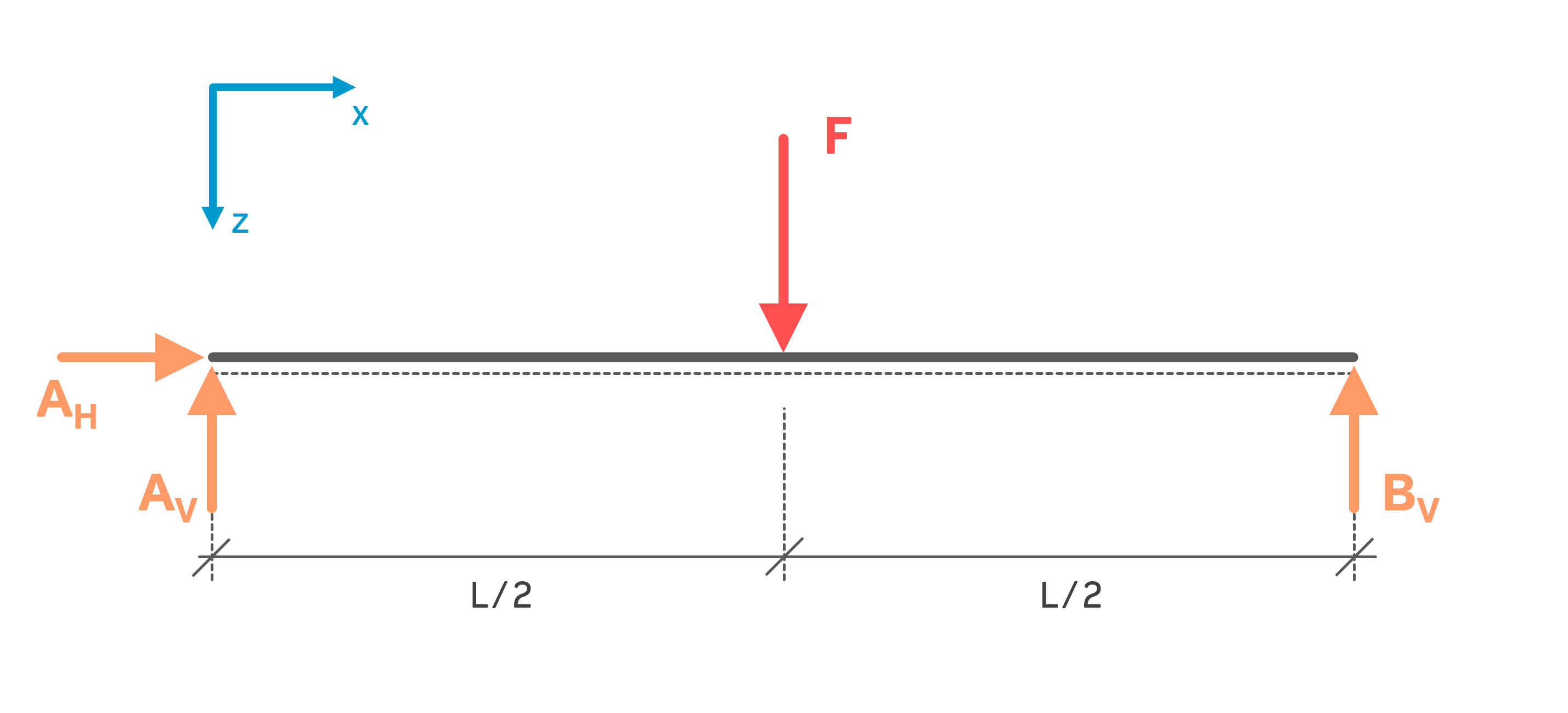
$$A_V=B_V=\frac{F}{2}=5\,kN$$ $$A_H=0$$
Schritt 2: Bereiche einteilen und Schneiden
Bevor der Balken geschnitten werden kann, muss zunächst geklärt werden, wo geschnitten werden muss. In den allermeisten Fällen gilt: Pro Bereich ein Schnitt. Um die Bereiche einzuteilen, hilft die folgende gedankliche Vorstellung:
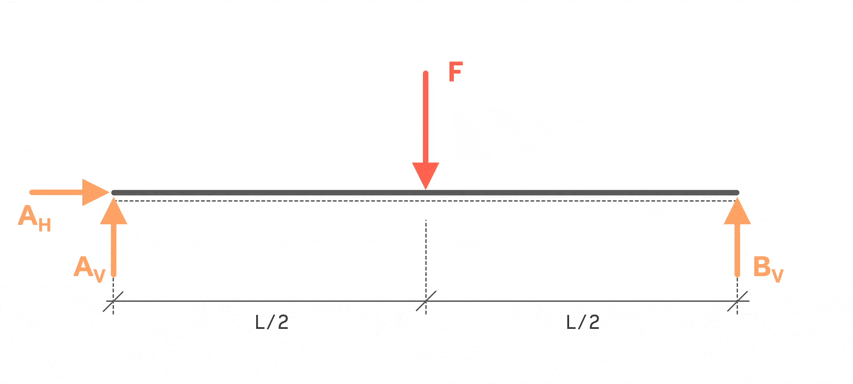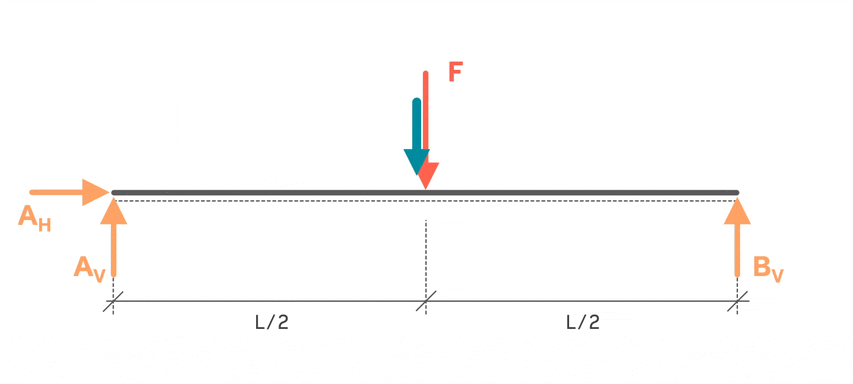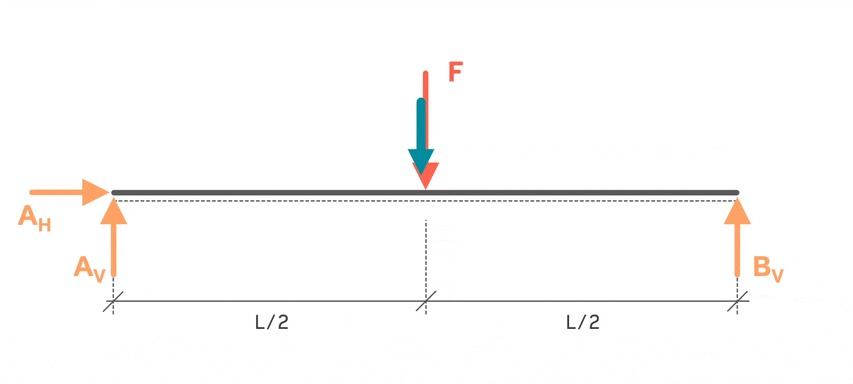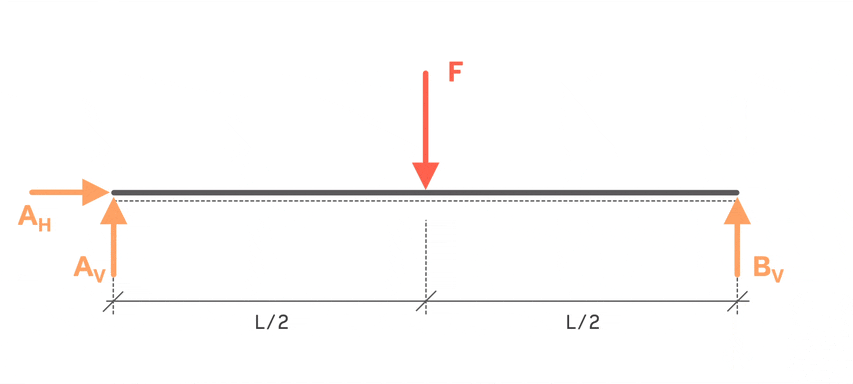
Am bestesten stellt man sich einen kleinen Spaziergang auf den Balken vor. Man startet, wie in der Animation zu sehen ist, links beim Festlager. Das ist der Beginn des 1. Bereichs. Dann läuft man so lange weiter, bis die erste Unterbrechung oder “Unstetigkeit” kommt. In unserem Fall ist es die Kraft F. Sobald man also vor der ersten Unterbrechung steht, endet damit der erste Bereich. Es geht weiter mit dem 2. Bereich. Hier läuft man wieder so lange, bis die nächste Unterbrechung kommt. Das wäre die Vertikalkraft vom Loslager (und auch das Ende vom Balken). An dieser Stelle endet der zweite Bereich. Weiter geht es nicht, deswegen ist die Bereichseinteilung damit abgeschlossen.
Pro Bereich ein Schnitt
Den Schnitt setzt man jeweils an einer beliebigen Stelle innerhalb des jeweiligen Bereichs (siehe folgende Abbildung). Schauen wir uns anhand des ersten Bereichs an, was das genau bedeutet: Der 1. Bereich ist insgesamt \( \frac{L}{2}=5\,m \) lang. Ich könnte (theoretisch) am Anfang bei \( x_1 \approx 0 \) oder auch am Ende bei \( x_1 \approx 5\,m \) schneiden. Ich könnte aber auch irgendwo dazwischen, an einer beliebigen Stelle \( x_1 \) schneiden, die sich zwischen \( 0 \) und \( 5\,m \) befindet. Mit derselben Überlegung kann man das Intervall im zweiten Bereich ermitteln.
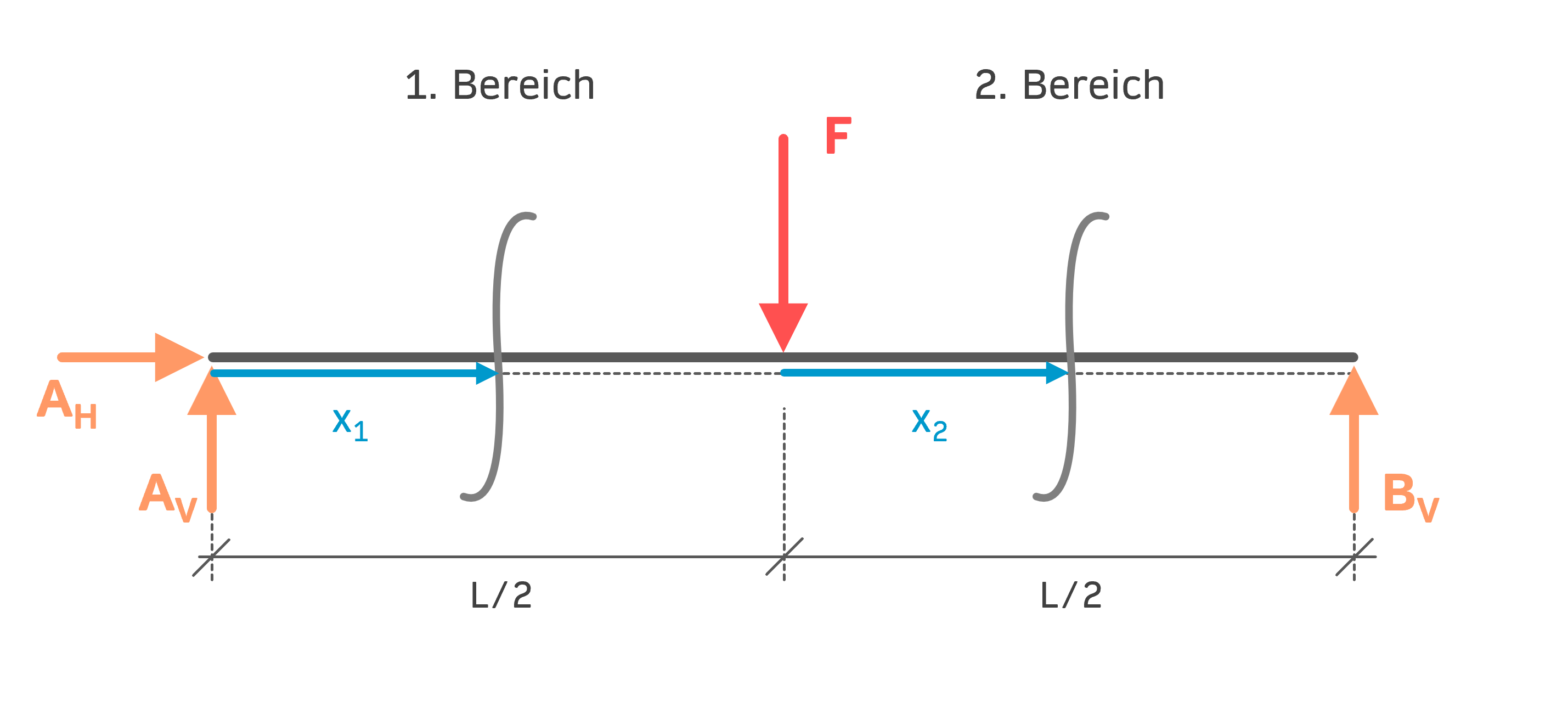
Für die Koordinaten ergibt sich daher:
$$ \, 0 < x_1 < \frac{L}{2} $$
$$ \, 0 < x_2 < \frac{L}{2} $$
Koordinaten richtig einzeichnen
Bei der Skizze für den Freischnitt muss im ersten Bereich die Koordinate \( x_1 \) zwingend am Anfang des Bereichs starten und bis zum Schnitt gehen. Dasselbe gilt auch für die Koordinate \( x_2 \) im zweiten Bereich. Das ist deshalb wichtig, damit später die Hebellängen beim Drehmoment korrekt bestimmt werden können.
Schritt 3: Gleichgewichtsbedingungen für jeden Bereich
Fangen wir mit dem 1. Bereich an: Grundsätzlich ist es für den 1. Bereich meistens sinnvoll, das positive Schnittufer (linkes Schnittufer) zu wählen, so wie in diesem Fall.
1. Bereich: \( \, 0 < x_1 < \frac{L}{2} \)
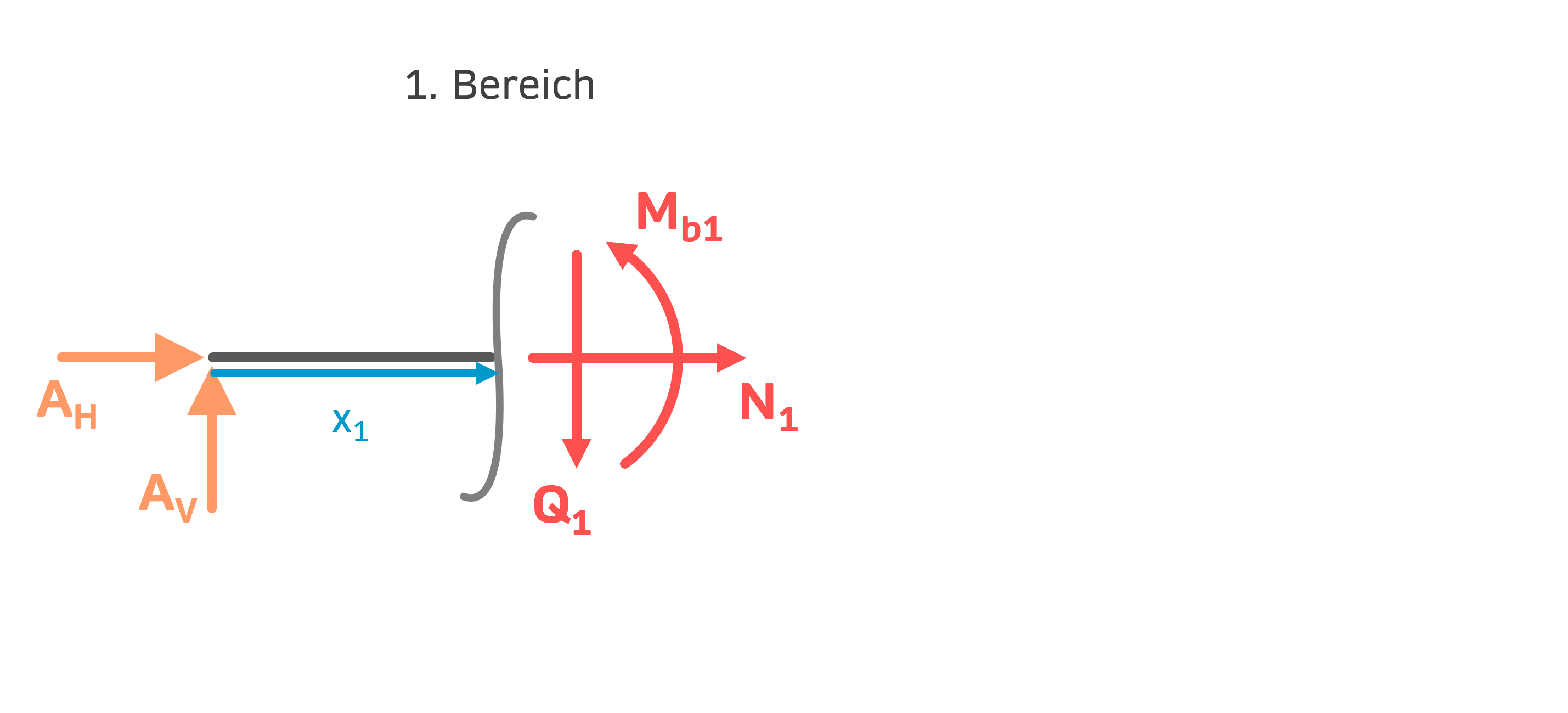
Aus den Gleichgewichtsbedingungen erhalten wir die gesuchten Schnittgrößen \( N,\:Q,\:M_b \).
Summe aller Kräfte in x-Richtung (Horizontalkräfte):
$$\sum F_H=0=N_1+A_H$$ $$\Rightarrow N_1=-A_H=0$$
Summe aller Kräfte in z-Richtung (Vertikalkräfte):
$$\sum F_V=0=Q_1-A_V$$ $$\Rightarrow Q_1=A_V$$ $$Q_1=\frac{F}{2}=5\,kN$$
Und schließlich noch das Momentengleichgewicht. Achtung: Bei den Schnittgrößen die Momentengleichung stets um den Schnitt \( S \) aufstellen.
Summe aller Momente um Schnitt S:
$$\sum M^S=0=M_{b1}-A_V \cdot x_1$$ $$\Rightarrow M_{b1}=A_V \cdot x_1$$ $$M_{b1}=\frac{F}{2} \cdot x_1$$
2. Bereich: \( \, 0 < x_2 < \frac{L}{2} \)
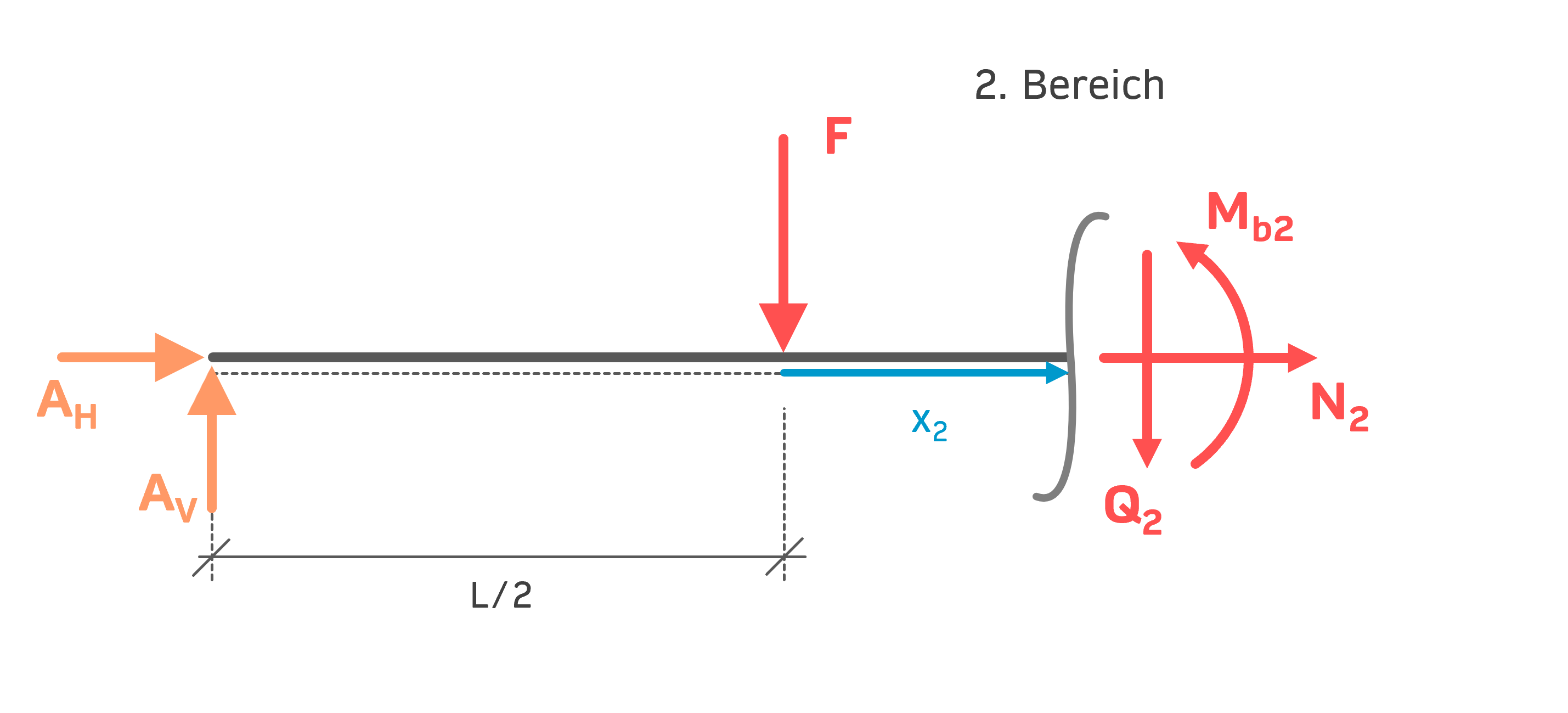
Summe aller Kräfte in x-Richtung (Horizontalkräfte):
$$\sum F_H=0=N_2+A_H$$ $$\Rightarrow N_2=-A_H=0$$
Summe aller Kräfte in z-Richtung (Vertikalkräfte):
$$\sum F_V=0=Q_2-A_V+F$$ $$\Rightarrow Q_2=A_V-F$$ $$Q_2=-\frac{F}{2}=-5\,kN$$
Summe aller Momente um Schnitt S:
$$\sum M^S=0=M_{b2}-A_V \cdot (\frac{L}{2}+x_2)+F \cdot x_2$$ $$\Rightarrow M_{b2}=A_V \cdot (\frac{L}{2}+x_2)-F \cdot x_2$$ $$M_{b2}=- \frac{F}{2} \cdot x_2 + \frac{F \cdot L}{4}$$
Schritt 4: Schnittgrößenverläufe zeichnen
Neben der Berechnung von Schnittgrößen ist auch die graphische Darstellung der Schnittgrößen wichtig: Schnittgrößenverläufe zeichnen (Beispiele). Und so sehen die Verläufe für die Normalkraft, Querkraft und für das Biegemoment aus:
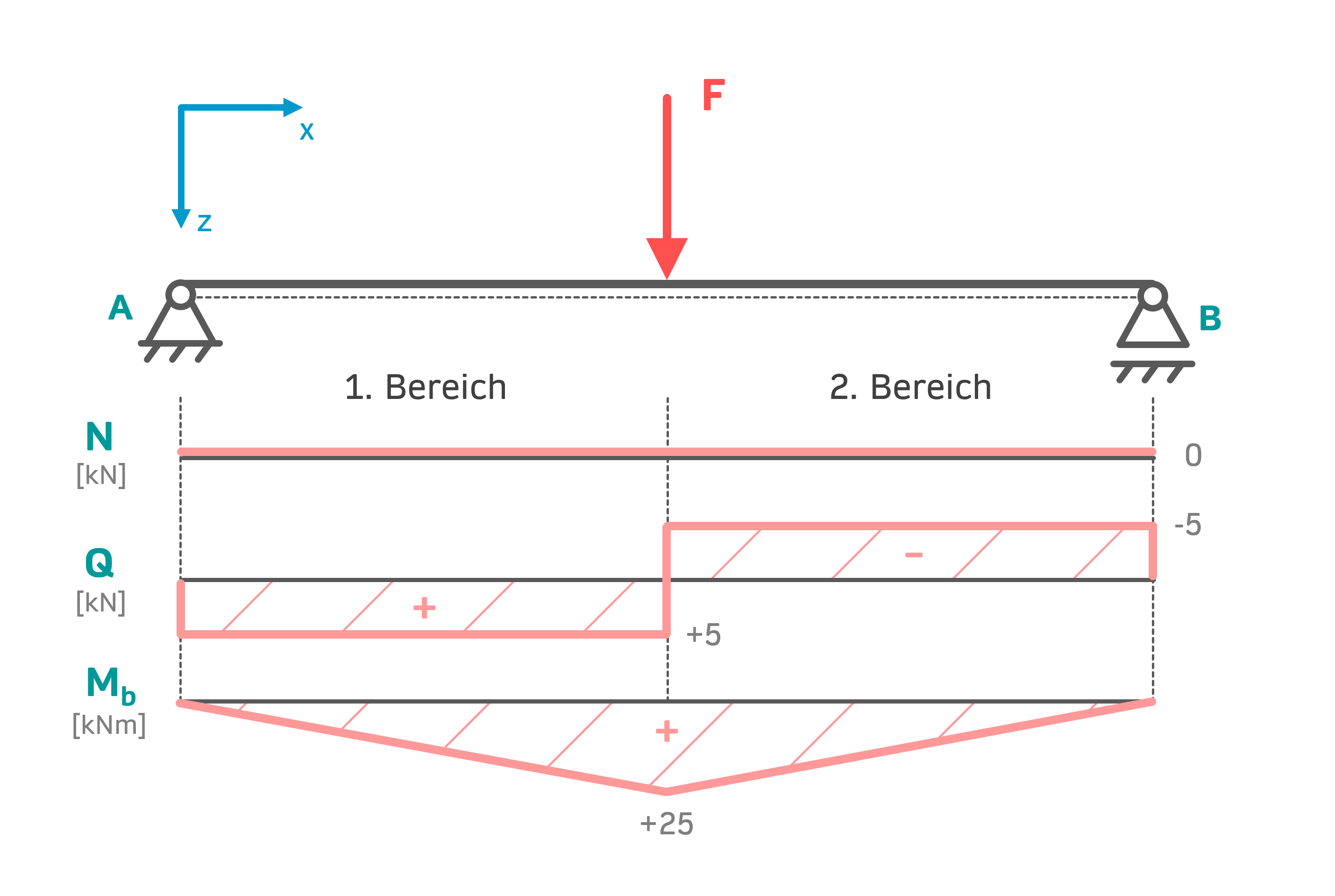
Normalkraftverlauf
Die Normalkraft ist im ersten und zweiten Bereich jeweils \( 0 \). Hier zeichnet man einfach eine Linie, die konstant über beide Bereiche \( 0 \) ist.
Querkraftverlauf
Die Querkraft ist im ersten Bereich konstant \( +5\,kN \) groß. Im zweiten Bereich ist sie konstant \( -5\,kN \) groß. Man zeichnet also die Querkraft, indem man im 1. Bereich eine konstante Linie bei \( +5\,kN \) und im 2. Bereich eine konstante Linie bei \( -5\,kN \) zeichnet. Am Übergang zwischen Bereich 1 und 2 macht der Querkraftverlauf einen Sprung in Höhe von \( F=10\,kN \). Dass der Sprung gerade so groß ist, wie die Kraft selbst, die an dieser Stelle den Balken belastet ist kein Zufall. Dort wo eine Einzellast wirkt, macht der Querkraftverlauf einen Sprung in Höhe der Kraft.
Momentenverlauf
In beiden Bereichen ist das Biegemoment linear. Das erkennt man daran, dass das \( x \) in den Momentengleichungen alleine für sich steht. Die Laufvariable \( x \) ist also weder im Quadrat noch in einer Wurzel. Lineare Funktionen sind gerade Linien. Eine gerade Linie zeichnet man am einfachsten, indem man Anfangs- und Endpunkt geradlinig miteinander verbindet. Das bedeutet, dass man in jedem Bereich das Biegemoment am Anfang des Bereichs und am Ende des Bereichs bestimmen muss. Im Anschluss daran werden Anfangs- und Endpunkte einfach miteinander verbunden.
Anfangs- und Endpunkt des Moments im ersten Bereichs:
$$M_{b1}(x_1=0)=0$$ $$ M_{b1}(x_1=5\,m)=25\,kNm$$
Anfangs- und Endpunkt des Moments im zweiten Bereichs:
$$M_{b2}(x_2=0)=25\,kNm$$ $$M_{b2}(x_2=5\,m)=0$$
Video: Schnittgrößen berechnen
Dieses Video erklärt nochmal Schritt für Schritt, wie Schnittgrößen berechnet werden. Es wird dieselbe Aufgabe (Fest-los-gelagerter Balken mit mittig wirkender Kraft) wie auf dieser Seite gerechnet.
Mit dem Laden des Videos akzeptieren Sie die Datenschutzerklärung von YouTube.
Mehr erfahren
Zusammenfassung
- Lagerkräfte berechnen
- Bereiche einteilen und schneiden (pro Bereich ein Schnitt)
- Für jeden Bereich die Gleichgewichtsbedingungen aufstellen (\( \Sigma\:M^S,\:\Sigma F_x,\:\Sigma F_y \)) und daraus die Schnittgrößen \( N,\:Q,\:M_b \) ermitteln
- Schnittgrößenverläufe zeichnen
Was man noch wissen sollte…
Wirkt eine Kraft auf einen Balken oder auf ein Bauteil, dann sind zwei Fragen für den Ingenieur wichtig.
- Wie muss ich meine Lagerung entwerfen, damit sie der Belastung standhält?
- Wie muss ich das Bauteil selbst entwerfen, damit es der Belastung standhält?
Nehmen wir eine Brücke als Beispiel. Die Lager der Brücke sind wichtig, damit die Brücke auf einem ordentlichen Fundament steht. Gerade um Flüsse herum stehen Brücken auf feuchte und weiche Böden. Man sollte daher wissen, mit welcher Kraft die Brücke auf den (feuchten) Boden wirkt, damit geeignete Gegenmaßnahmen getroffen werden können. Um das zu klären, berechnet man die Lagerkräfte. Auf der anderen Seite gibt es noch die Schnittgrößen. Sie sind nun dafür zuständig, dass die eigentliche Brücke (also die Fahrbahn) korrekt bzw. stark genug ausgelegt wird. Anhand der Schnittgrößen kann man nämlich ablesen, welche inneren Belastungen hervorgerufen werden (wenn zum Beispiel eine schwerer LKW auf der Brücke fährt). Und aus diesen wiederum kann man dann eine passende Konstruktion entwerfen, die den Belastungen standhält.
Verwandte Themen
Grundbegriffe Schnittgrößen
Schnittgrößenverläufe zeichnen (Beispiele)
Lagerkräfte berechnen: Prüfungsaufgabe
Oder zurück zur Themenübersicht: Technische Mechanik 1
