---

Wie definiert man den Schwerpunkt?

Der Schwerpunkt befindet sich dort, wo man seinen Zeigefinger positionieren müsste, um den Körper oder die Fläche zu balancieren. In der Technischen Mechanik definiert man den Schwerpunkt ähnlich, nur umständlicher formuliert: Der Schwerpunkt eines Körpers gibt an, wo die resultierende Gewichtskraft des Körpers angreift.

---

Tabelle mit wichtigen Schwerpunkten

Fläche	Flächeninhalt	Lage des Schwerpunktes
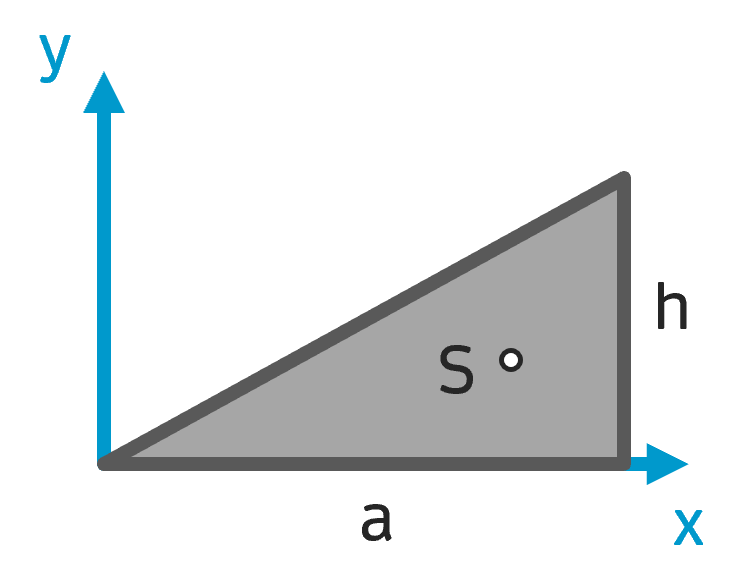Schwerpunkt Dreieck	$$ A = \frac{1}{2} a \cdot h $$	$$ x_S = \frac{2}{3} a $$ $$ y_S = \frac{1}{3} h $$
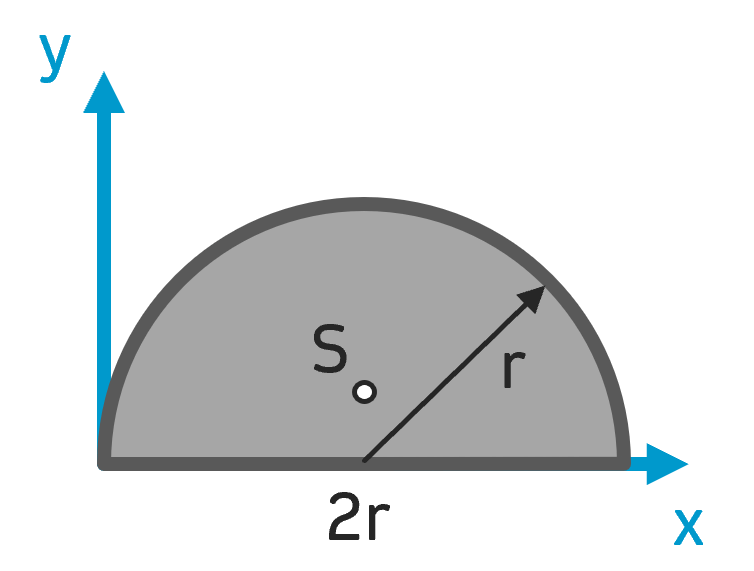Schwerpunkt Halbkreis	$$ A = \frac{\pi}{2} \cdot r^2 $$	$$ x_S = r $$ $$ y_S = \frac{4r}{3 \pi} $$ Schwerpunkt liegt auf der Symmetrieachse
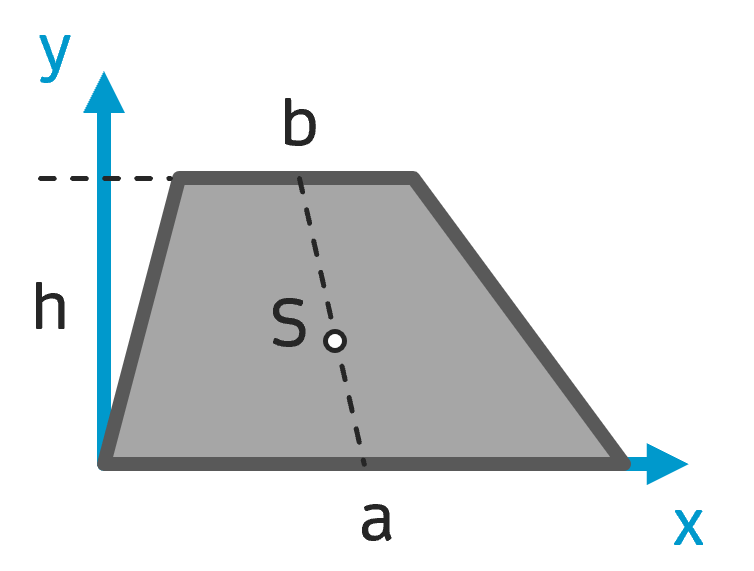Schwerpunkt Trapez	$$ A = \frac{h}{2} \cdot (a+b) $$	$$ y_S = \frac{h}{3} \cdot \frac{a+2b}{a+b} $$ Schwerpunkt liegt auf der Seitenhalbierenden
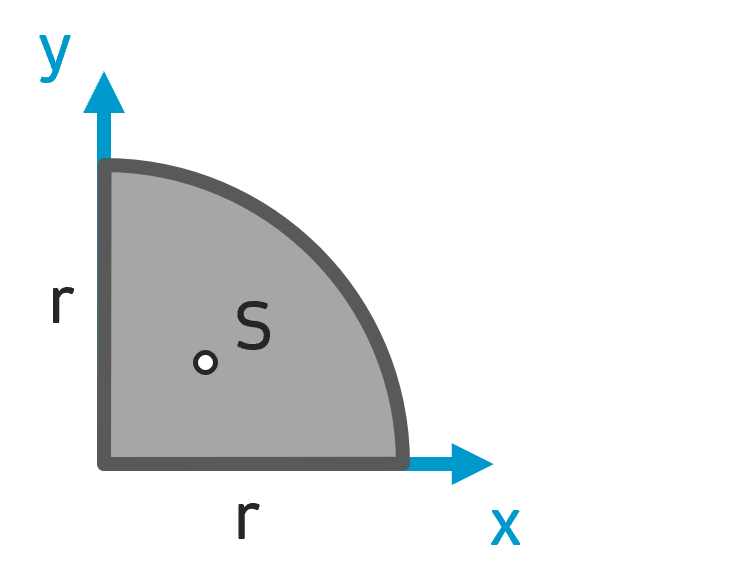Schwerpunkt Viertelkreis	$$ A = \frac{\pi}{4} \cdot r^2 $$	$$ x_S = \frac{4r}{3 \pi} $$ $$ y_S = \frac{4r}{3 \pi} $$
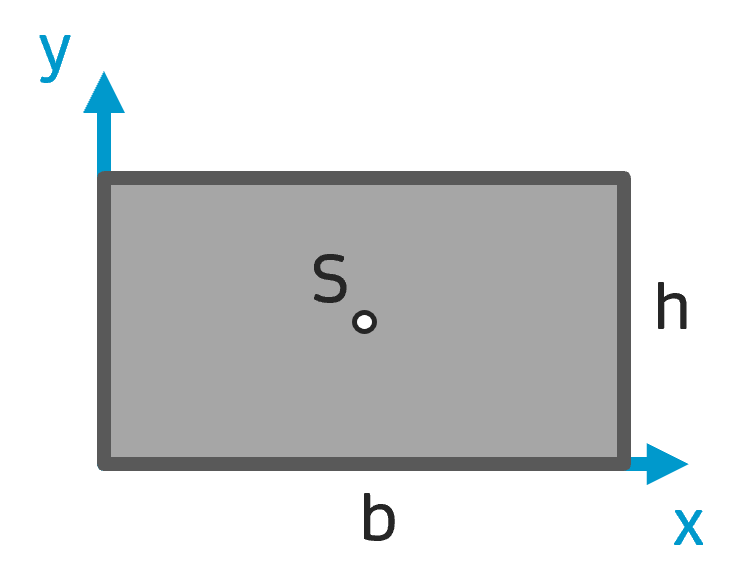Schwerpunkt Rechteck	$$ A = b \cdot h $$	$$ x_S = \frac{b}{2} $$ $$ y_S = \frac{h}{2} $$

---

FAQ: Schwerpunkt berechnen

Wie berechnet man den Schwerpunkt?

Der Flächenschwerpunkt (genauer: die Lage des Schwerpunktes) kann mit dieser Formel berechnet werden:

$$x_S = \frac{\sum A_i \cdot x_{Si}}{\sum A_i} = \frac{ A_1 \cdot x_{S1} + A_2 \cdot x_{S2} + …}{A_1 + A_2 + …}$$ $$y_S = \frac{\sum A_i \cdot y_{Si}}{\sum A_i} = \frac{ A_1 \cdot y_{S1} + A_2 \cdot y_{S2} + …}{A_1 + A_2 + …}$$
Hier findest du ein ausführliches Rechenbeispiel: Schwerpunkt berechnen: Prüfungsaufgabe

---

Wie berechnet man den Schwerpunkt mit der Tabelle?

Man kann den Schwerpunkt einer Fläche auch mit dem Tabellenverfahren bestimmen. Dafür füllt man zuerst die folgende Tabelle aus.

\[
\begin{array}{|c|c|c|}
\hline
\text{\( i \)} & \text{\( A_i \)} & \text{\( x_{Si} \)} & \text{\( y_{Si} \)} & \text{\( A_i \cdot x_{Si} \)} & \text{\( A_i \cdot y_{Si} \)} \\
\hline
1 & & & & & \\
\hline
2 & & & & & \\
\hline
… & & & & & \\
\hline
\sum & \text{\( A \)} & \text{-} & \text{-} & \text{\( B \)} & \text{\( C \)} \\
\hline
\end{array}
\]

Im Anschluss daran erhält man die Koordinaten des Schwerpunkts ganz einfach mit:
$$x_S = \frac{B}{A}$$ $$y_S = \frac{C}{A}$$
Ausführliches Rechenbeispiel: Schwerpunkt berechnen mit dem Tabellenverfahren

---

Was mache ich, wenn bei einer Fläche ein Stück fehlt?

Wenn eine Teilfläche aus einer zusammengesetzten Fläche fehlt, dann geht der Flächeninhalt dieser Teilfläche negativ in die Berechnung ein. Die Schwerpunktskoordinaten einer fehlenden Teilfläche werden allerdings nicht negativ, nur weil die Fläche ausgeschnitten wurde. Hier müssen die Koordinaten genauso abgelesen werden, wie bei “positiven” Teilflächen. Ein ausführliches Rechenbeispiel mit ausgeschnittenen Teilflächen findest du hier: Schwerpunkt berechnen mit negativen Teilflächen

---

Wo befindet sich der Schwerpunkt?

Der Schwerpunkt eines Körpers ist dort, wo die Gewichtskraft des Körpers wirkt. Mit meinen Worten:

Der Schwerpunkt ist dort, wo man seinen Zeigefinger halten müsste, um den Körper zu balancieren.

Wer schon mal beim Warten auf das Essen versucht hat, die Gabel mit einem Finger in Balance zu bringen, hatte bereits das Vergnügen gehabt, den Schwerpunkt (experimentell) zu bestimmen.

---

Video: Schwerpunkt berechnen

In diesem Video wird Schritt für Schritt erklärt, wie der Schwerpunkt einer zusammengesetzten Fläche berechnet wird (mit und ohne das Tabellenverfahren).

---

Verwandte Themen

Schwerpunkt berechnen: Prüfungsaufgabe
Streckenlast berechnen: Formeln und Überblick
Oder zurück zur Themenübersicht: Technische Mechanik 1